PLO:【密码专栏】超强进阶：PLONK VS Groth16（上）_ROTTO币

前言

前文《天冷了，干了这碗“零知识证明”鸡汤》对「零知识证明学习」作了一个形象化的比喻：炖鸡汤。那么本系列的主要内容可以简单概括为《论高压锅炖鸡汤的一百种方法》之方法二。在学会了“清炖鸡汤”之后，不如来一口“阿胶鸡汤”补补脑细胞吧！

正如鸡汤不同风味之间各具千秋，不同的zk-SNARK方案也各有所长。zk-SNARK方案可以被分为与zk-SNARK，PLONK与Groth16分别是其中的典型代表。通过本系列，我们将对PLONK算法内容作简要介绍，并指出PLONK和Groth16算法思路上的异同。

PLONK算法在中提出，由来自于ProtocolLabs的研究员Gabizon和以太坊隐私交易协议AztecProtocol的两名研究人员合作完成。PLONK的提出晚于Groth16，在证明和验证的性能上与Groth16也存在一定差距，但是基于通用可更新的可信设置这一特点，使PLONK算法在零知识证明领域占据了一席之地。

可信设置

可信设置可以说是PLONK和Groth16两者间最显著的差异。正是为了避免一次性的可信设置，PLONK设计了后续的约束系统和问题压缩方式。那么什么是零知识证明中的可信设置呢？可信设置实际上是在创建一个用于证明验证的秘密，任何知道这个秘密的人都可以伪造证明通过验证。如果将零知识证明看作是一扇挡在证明者a和验证者b之间上锁的门，那么合法构建的证明就是可以打开门的口令，a提供口令即可进入房间。但是如果a得知了门的秘密也就是房间窗户的位置，那么a可以直接无视锁的存在翻窗进入房间。

数据：0x8b9和0x362开头鲸鱼地址共买入788,877枚LINK:金色财经报道，Spot On Chain监测显示，在过去的45分钟内，0x8b9和0x362开头的鲸鱼地址（可能是同一巨鲸）共同交换了3,146枚stETH和ETH（572万美元），以7.25美元的平均价格购买了788,877枚LINK。自他们购买以来，LINK的价格从7.12美元飙升至7.5美元，涨幅约为7%。[2023/7/20 11:07:05]

▲无窗的房间

显然，最安全的做法是找一个「没有窗的房间」，这也是一部分零知识证明方案的思路——无需可信设置，例如可扩展透明知识论证zk-STARKs和防弹证明Bulletproofs。虽然它们的安全性得到提高，但是目前这类方法的证明验证性能是远低于zk-SNARKs的，近线性的验证和规模较大的证明使其不适用于很多场景。

▲窗户位置指定策略

PLONK和Groth16的做法都是保留窗户，但是尽力保护窗户的位置不被别人知道。

Groth16的做法是：根据不同的问题，每次都指定窗户在房间中的摆放位置，也就是它需要一次性的可信设置。而PLONK面对不同的问题时：窗户的位置是固定不变的，即窗户的位置只需要被指定一次。也就是说PLONK的可信设置是通用的。那么这些窗户指定的位置由谁来确定呢？当然，可信第三方是一个备选项。但这意味着说这间房间是否会被恶意证明者攻破，其安全性寄希望于这位第三方。除此之外还有一项热门技术也可为其提供思路——多方安全计算。沿用之前的例子，可以不太严谨地将MPC概括为：多个人共同指定窗户的位置，除非这些参与者全部联合起来对答案，这个位置将无法由任何人得知。

BiSwap：已检测并解决Migrator合约漏洞，请勿与访问该合约，用户资金安全:7月1日消息，BSC跨链交易平台BiSwap今日凌晨在推特上表示，团队检测并解决了Migrator合约漏洞。Biswap V2和V3 AMM协议上的资产是安全的。团队阻止通过网站访问迁移过程，因为Migrator合约已被利用，不要试图直接访问本合约，如尚未这样做，请撤销对这些合约的批准。正在更详细地审查此漏洞的结果，后续将发布报告。用户资金是安全的，上述漏洞与AMM V2和V3资金无关。[2023/7/1 22:12:23]

显然，使用MPC时，参与者的数量越多，秘密的安全性越高，这类可信设置也比可信第三方更为用户所接受。遗憾的是，虽然目前提出了基于Groth16的可信设置，但是由于Groth16的秘密计算与特定的问题相关联，每次遇到新的问题时，必须重新开启一轮MPC可信设置。可想而知，需要多方参与的计算协议将是极为繁琐的，这样将大大影响Groth16的性能。相比之下，具备通用性的PLONK与MPC的适配度极高。

而之前提到的PLONK可信设置的可更新性则是指：通用的PLONK秘密可以通过再开启一轮MPC作更新。新生成的秘密安全性建立在两次MPC的安全性上，只要两次中有一个参与者是诚实的，这个秘密就是可信的。约束系统

Groth16及PLONK均将程序先转化为一个由加法门和乘法门组成的算术电路，再通过将电路构建为多项式的形式来进行后续的计算。本节我们将使用Vitalik文章中的一个简单例子进行说明：

SEC助理总会计师：币安在2021年向Paxos的一家外国子公司转移了近200亿美元的混合资金:金色财经报道，美国证券交易委员会（SEC）助理总会计师 Sachin Verma 发表声明称，币安在 2021 年向Paxos的一家外国子公司转移了近 200 亿美元的混合资金。Binance.US 以 BAM Trading 的名义和其他几个与 Binance 相关的账户从 Silvergate Bank 的账户向一家名为 Merit Peak Ltd 的贸易公司发送了数百万美元的混合资金。例如，在 2021 年，来自 Key Vision（110.5 亿美元）、Prime Trust（11 亿美元）（通过 BAM Trading）和 Bifinity UAB（63 亿美元）（通过 Binance Holdings Limited）的资金被转移到 Merit Peak，Merit Peak 全部转移这笔钱是其在 2021 年向 Paxos 的一家外国子公司转移近 200 亿美元。[2023/6/8 21:22:50]

对于程序qeval,prover需要证明自己知道qeval(x)=35的解，即x=3。

defqeval(x):

y=x**3

returnx+y+5，其转化为算术电路可表示如下：

亚马逊云正与Cronos Labs合作支持Web3初创公司:金色财经报道，AWS Hong Kong发推称，亚马逊云正在与Cronos Labs合作，以支持Web3初创公司通过Cronos加速器计划扩展和发展，推动DeFi、GameFi、SocialFi等应用程序发展。[2023/4/26 14:27:30]

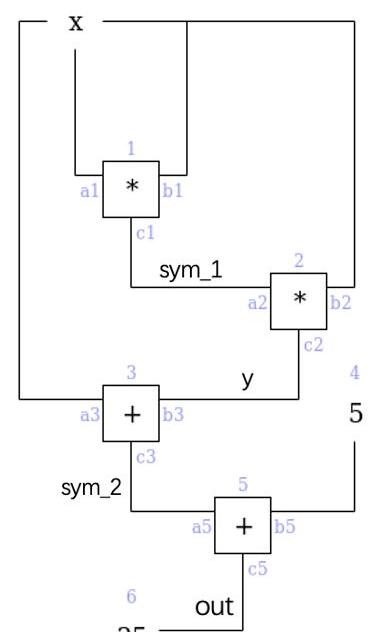
PLONK中，上图电路的描述由两部分组成：门约束与线约束。门约束固定电路中每个门的动作。此外，在电路中我们规定相连线的值应保持一致，对此线约束规定这些线的关系。接下来我们分别讨论两类约束的多项式表示。门约束

在PLONK中，对于第i个门，可被描述为如下形式：

（QLi)ai+(QRi)bi+(QOi)ci+(QMi)aibi+Qci=0

其中Q均为常数，a,b,c则是信号的下标。具体地，在PLONK中门约束可以被分为三类：算术约束、布尔约束、公共输入约束。

最为常见，用于表示电路中的所有加法门和乘法门，此时a,b,c分别表示门的左右输入和输出信号下标，Q_C一般为0。根据门的类型剩余的符号有不同的取值：

数据：Arbitrum生态总交易和合约日志份额占比GMX排名第一:金色财经报道，据 Nansen 数据，Arbitrum 生态协议中，总交易和合约日志份额占比 GMX 排名第一，占比 22%，Treasure 以 19% 份额排名第二。Sushiswap、Uniswap 以 Hop 分列 3 至 5 位。[2023/3/17 13:10:06]

加法门：QLi=1，QRi=1，QOi=-1，QMi=0??ai+bi-ci=0乘法门：QLi=0，QRi=0，QOi=-1，QMi=1-ci+?aibi=0

顾名思义，用于约束布尔类型的信号，其值只能取0或1。例如现在需要约束下标为j的信号∈{0,1}，那么门约束式子中各变量的取值为：

ai=bi=j，QLi=-1，QMi=1，QOi=QRi=Qci=0

-j+j*j=0

另外，针对问题中出现的证明方和验证方都知道取值的输入，需要在约束系统中有所体现。例如要求约束下标j的信号取值为v，对应的取值为：

ai=j，QLi=1，QMi=QOi=QOi=0，Qci=-v

j-v=0

利用该式，我们可以很容易地表示上图中的所有门约束：

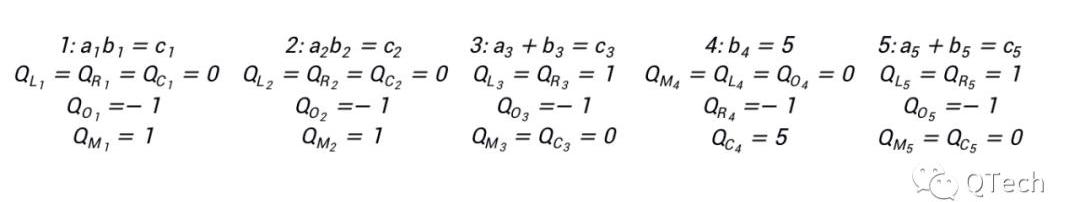
与Groth16类似，可以将所有的多项式组整合在一个多项式中：

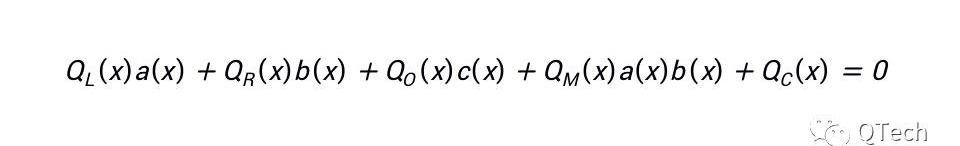
线约束

线约束可以分为两种情况：

同一多项式内部，例如：a1=a3

不同多项式之间，例如：a1=b1

当只需要考虑情况1时，可以通过构造p(x)=P(x)来实现约束：

X(X)=X

p(X+1)=p(X)*(β*X(X))+Y(X)+γ）

P(X+1)=P(X)*(β*X(σ(X))+Y(X)+γ）

p(0)=P(0)=1

其中β,γ为随机数，X->Y表示了待约束的多项式，P(x)使用了x的置换σ(x)。对于下面例子：

X(1)→Y(1)

X→Y：X(2)?→?Y(2)?and，Y(1)=Y(3)

X(3)→?Y(3)

σ(1)=3

σ(X)：σ(2)=2

σ(3)=1

当且仅当Y(1)=Y(3)成立时，p(x)=P(x)。

现在，让我们增加问题的复杂度：需要约束的多项式个数为k时。自然地，设门的总数为n，我们可以对第j个多项式构造对应的p_j(x)=P_j(x)，即

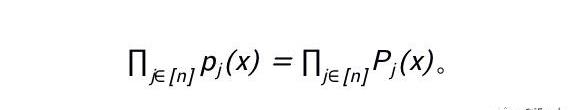
进一步地，情况2的出现要求对以下情况中的x作区分：

pj(x)and?pi(x)????

那么可以增加对x的映射，对于第j个多项式：

X(X)=(j-1)*n+X

p(X+1)=p(X)*(β*X(X))+Y(X)+γ）

P(X+1)=P(X)*(β*X(σ(X))+Y(X)+γ）

p(0)=P(0)=1

以上就是线约束的全部内容，其实质是为了保证电路中同一条或相连线上的值相等。

与Groth16类似，将上述的约束联立将得到一个完整的PLONK约束系统。通过将抽象的代码和电路转化为约束系统R1CS，我们可以将一个零知识证明问题固定下来。让我们带着问题进入下篇：PLONK中如何将R1CS转为多项式描述？它与Groth16做法区别在何处？敬请期待！

ArielGabizonandZacharyJ.WilliamsonandOanaCiobotaru.(2019).PLONK:PermutationsoverLagrange-basesforOecumenicalNoninteractiveargumentsofKnowledge.

SeanBoweand?ArielGabizonandIanMiers.(2017).ScalableMulti-partyComputationforzk-SNARKParametersintheRandomBeaconModel.

https://vitalik.ca/general/2019/09/22/plonk.html

标签：PLOLONROTGROETHPLOPoloniexROTTO币squidgrow币发行价

Gateio热门资讯