PLO:密码专栏 | 超强进阶：PLONK VS Groth16（下）_ROT

前言

本篇是“PLONKVSGroth16”的下篇，在上篇中我们对PLONK作了简要介绍，分析了PLONK和Groth16算法在「可信验证」和「约束构建」上的异同。那么，接下来让我们一起看看在后续的「证明生成」和「验证阶段」两者将有怎样的差异，以及整体上的性能区别。

证明生成

对于程序qeval,prover需要证明自己知道qeval(x)=35的解，即x=3。

defqeval(x):

y=x**3

returnx+y+5

在上篇中我们已经介绍了PLONK的约束形式：门约束与线约束。继续使用之前的例子，约束意味着零知识证明系统将这个问题约束成了一组格式固定的数学表达式，即问题描述等价于约束描述。而如果证明者真的知道这个问题的答案，将答案和计算中的中间参数代入约束表达式，这个组表达式必将是成立的。反之，如果该Prover提供的一组解无法使表达式成立，说明prover并不具备关于该问题解的知识。

这是最朴素的证明验证思路，可以将它看作是“锁”和“钥匙的配对“：该问题约束的构建类似于“打造门锁“，而针对该问题提供的一组解信息就是”一把开启门锁的钥匙“。显然，Prover可以举着自己的解交给验证者来验证。可是这违背了我们的零知识原则：Verifier不应该获取到Prover的隐私信息。

Monero恶意软件升级，现可以窃取密码接管挖矿:网络安全公司Unit42的一份报告称，黑客们已经更新了Monero（门罗币）长期运行的恶意软件“Black-T”，以窃取用户证书，并接管受感染电脑上的任何其他非法挖矿软件。这样的恶意软件行为是以前从未见过的。Black-T现在可以找到受害者计算机上的敏感用户信息，并将其发送给黑客，黑客可以利用非法获取的信息进行进一步攻击。这些信息包括但不限于密码、在线凭证和银行账户详细信息。报告称，Black-T使用一种名为“Mimikatz”的黑客工具从Windows操作系统中窃取明文密码。该工具还允许攻击者劫持用户会话，例如当用户处于活动状态时中断计算机使用。此外，如果Black-T发现任何已经存在加密挖矿恶意软件的计算机，它会自动攻击这些文件并禁用挖矿软件，然后安装自己的加密劫持程序。（Decrypt）[2020/10/6]

那么有什么方法能在解锁的同时保护隐私信息呢？

这里我们用到一个简单的数学小技巧：减除，对此不太了解的读者可查阅文章最后的前置知识。在前文《超强进阶：PLONKVSGroth16》我们已经对从约束系统转化到多项式进行了详细的描述，在此我们不再赘述具体的转化过程，但需要重复的一点是：根据生成时使用的点值对，生成的多项式在这些点处的取值将恒为0。PLONK同理，此处我们给出两种算法的约束系统转化为多项式后的形式。

动态 | 天风证券：官方确立PKI密码技术将在区块链等领域应用，预计新增市场规模接近100亿元:据数据宝消息，我国首部密码领域法律即将正式实施。天风证券（601162.SH）表示，密码产业链主要包括TO G建设方、TO B运营商。TO G行业容量从10亿级扩大至约50亿级，增长中枢提升至30%以上。官方确立PKI密码技术将在物联网、区块链、安可、电子签名领域应用。据其测算，新增市场规模接近100亿元，是行业厂商收入的数十倍。注：我国首部《密码法》将于2020年1月1日起施行。[2019/12/25]

Groth16:

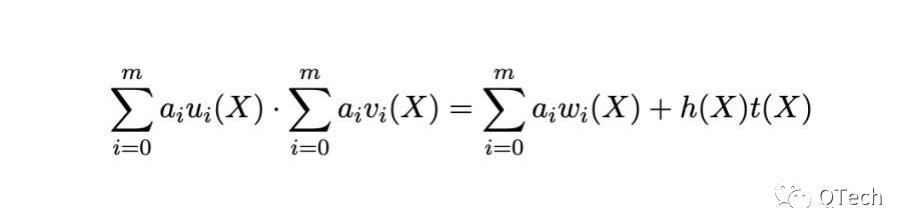
PLONK:?我们设门约束多项式为D(X)，线约束多项式为L(X)，那么PLONK的整个约束多项式将被表示为：

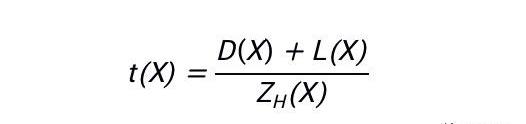
动态 | 一比特币投资者因密码问题无法登陆账户，账户余额近1300万美元:据Cointelegraph今日消息，一位比特币投资者因输入密码无效而无法登陆账户，该账户有1800枚比特币，价值超过1290万美元。账户名为u/lumanubrecon的用户称，至26日，其账户中的1800枚比特币已无法获取。2016年，该用户将这些比特币存储在所谓的“brain wallet”中，当使用当时生成的密码短语来恢复钱包时，该钱包却并未解锁。据悉，brain wallet通常没有密码短语的物理或数字记录，其用户会创建了一个容易记忆但难以破解的密码。 u / lumanubrecon在随附的帖子中解释道，“除记住密码短语外，我还把它写了下来，然而，输入密码后，它并未生成我存储1800个比特币的地址。”[2019/11/26]

可以看到，两者都使用了减除的思路，也就是这里的h(X)和ZH(X)，其具体内容取决于构建约束多项式时取的点值。

证明与验证

同样在之前的文章中，我们可以看到Groth16的证明规模极小，只包含三个群元素A,B,C。然而，这样优雅的证明实现依赖于它的非通用可信设置，这也是Groth16的一大痛点。在Groth16中，证明方提供A，B，C，验证方基于可信设置提供的参数，构建一个配对验证等式。在验证过程中包含了三次配对操作，也就是对验证性能影响较大的耗时运算。Groth16的具体证明验证如下所示。

分析 | 彭博社：极少的商业银行为密码货币行业提供服务:据彭博社报道称，尽管像摩根大通这样的华尔街传统金融机构已经宣布将推出 JPM Coin 数字货币用于内部结算，但是实际上，像汇丰、摩根大通这样的主流大型金融机构依然拒绝为密码货币相关企业提供基本的银行服务，只有极少的商业银行可以为密码货币行业提供服务，其中包括总部位于美国加州圣迭戈的 Silvergate 银行，该银行与密码货币业务相关的存款已经达到 400 亿美元，以及美国的 Signature 银行和欧洲的 Frick 银行。另外，区块链项目只能寻找替代途径解决基本的需求。比如总部在香港的交易所 CoinFLEX，只能选择向员工发放稳定币 Tether 为替代方案，解决发放薪酬的现金需要。[2019/3/4]

Groth16证明：

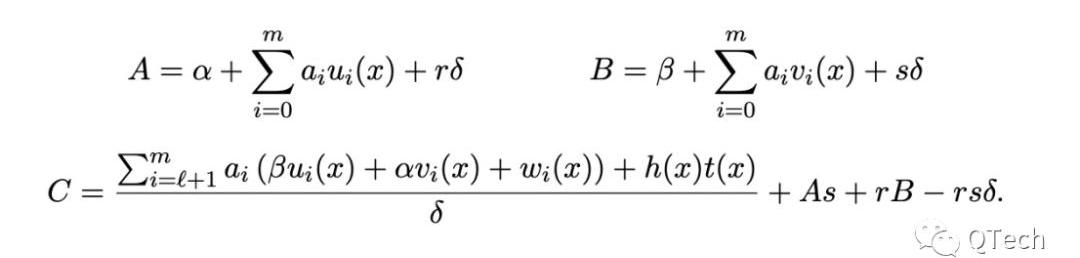
Groth16验证：

斯坦福大学应用密码学小组提出可减少区块链数据的方法:斯坦福大学(Stanford University)应用密码学小组(ACG)提出了一种可以大幅减少区块链数据的方法，数据大约可以被减少10倍，希望实现比特币和其他加密货币的高效交易。[2017/11/21]

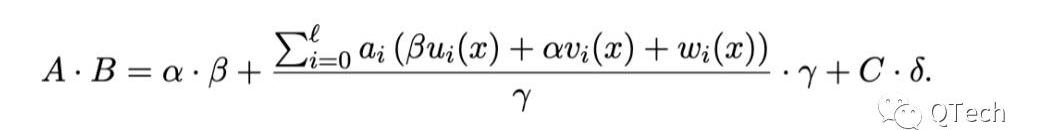
相比之下，PLONK的证明验证将会复杂得多，这也是使用通用可信设置付出的代价。从验证方角度看，由于可信设置参数缺少了包含问题具体内容，从而无法帮助其构建一些制约证明多项式的值。因此，如何固定住证明多项式的内容成为一个难题。PLONK使用的一个思路是引入Kate承诺。

结合前述的约束多项式，我们可以对t(x)中出现的每一项都构建一个承诺，以实现验证方的验证。PLONK证明的具体内容如下，包含了两个点处的验证：Wz(X)为多个多项式的同点承诺，Wzw(X)则为另一个点处的对z(X)的承诺。

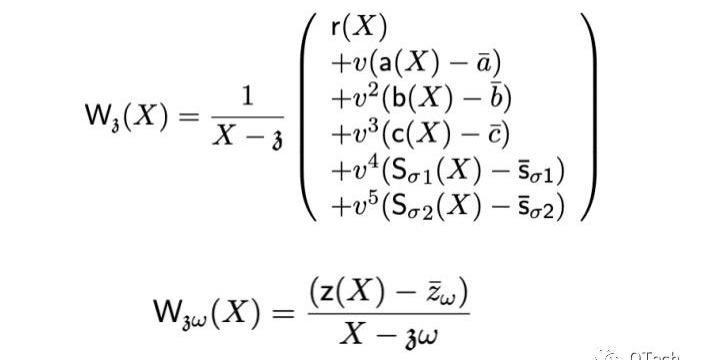
最后，PLONK的验证在原文中也被归纳为一个简洁的公式，实际上就是将上面提到的两个点处的承诺简单相加，具体等式如下所示：

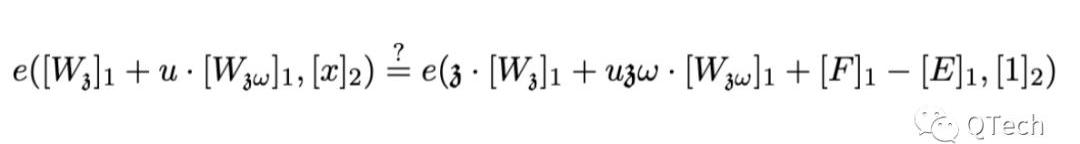
以上就是PLONK和Groth16算法内容的具体对比结果，讲了这么多冗长的公式变换，两者在性能层面的差距究竟如何呢？

性能比较

在这里我们给出的是PLONK论文中的结论。Table1是在证明阶段的一个性能比较，Table2则是验证阶段的性能。可以看出，在验证上，两者的差距不大，Groth16比PLONK多了一次配对运算；而在证明方面我们遗憾地发现，Groth16不论在证明的工作量还是证明长度上仍然保持着最优的性能。但需要指出的是PLONK，尤其当它工作在fast模式时，所使用的SRS长度是所有算法中最短的。

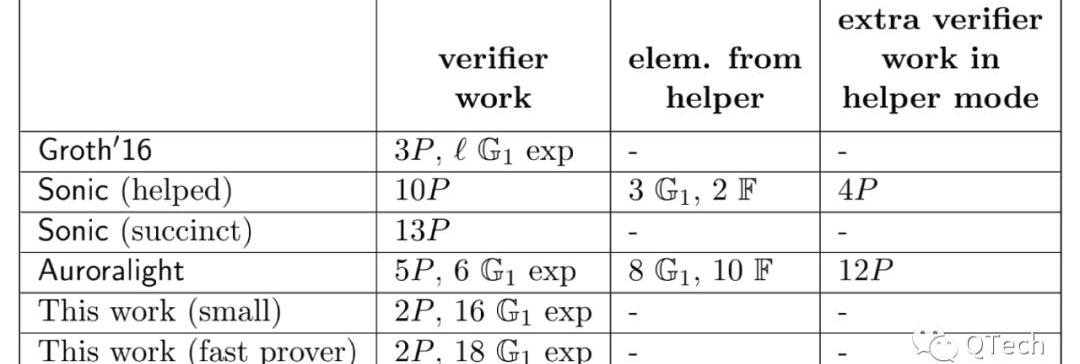
▲验证阶段性能比较

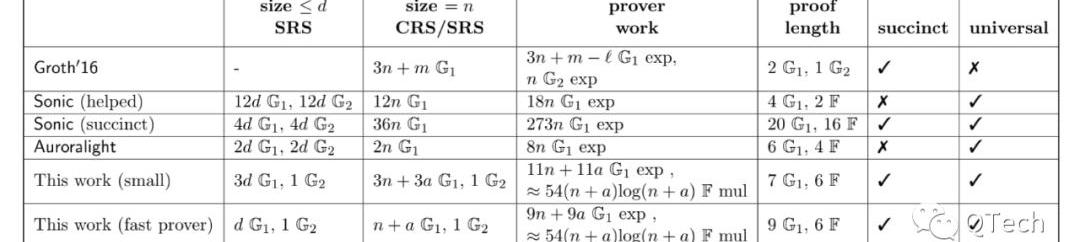
▲证明阶段性能比较

前置知识

多项式减除

顾名思义，化减为除：若我们需要证明一个多项式f(x)在点a的取值为b，也就是证明f(a)-b=0；那么我们可以将其转换为证明多项式f(x)-b可以整除(x-a)。其数学表示：

设多项式f(x)且f(a)=b，则存在一个多项式g(x)，使得：f(x)-b=g(x)(x-a)

kate承诺Kate承诺是由Kate，Zaverucha和Goldberg在2010年提出的一种多项式承诺方案。Kate承诺有多种形式，本文仅介绍PLONK中使用的常用形式，详细可参考其paper中的相应内容。其常用形式可以概括为对多项式的隐藏和部分打开验证。针对多项式f(x)，Kate承诺的具体步骤如下：

1）构造f(x)在点a处的承诺C

C：f(a)

2）选取点z，执行f(z)的opening

gz(x)=f(x)-f(z)/x-z

wz=gz(x)

3）给定f(z),C和Wz，验证Kate承诺

C=wz*(a-z)+f(z)

以上就是“PLONKVSGroth16”的全部内容，如有任何疑问，欢迎添加小助手桔子加入技术交流群，在这里，你想知道的都会得到解答～

A.Kate,G.M.Zaverucha,andI.Goldberg.Constant-sizecommitmentstopolynomialsandtheirapplications.pages177–194,2010.

ArielGabizonandZacharyJ.WilliamsonandOanaCiobotaru.PLONK:PermutationsoverLagrange-basesforOecumenicalNoninteractiveargumentsofKnowledge.2019.

标签：PLOLONGROROTExploit Networkpoloniex清退大陆用户怎么用Hamster GroomersChord Protocol

Uniswap热门资讯