区块链:技术入门 | 深入理解零知识证明算法之Zk-stark：Low Degree Testing_blockchainresearchandapplication

前言

本系列的第二篇文章，以超市收据为例，描述了Arithmetization的具体过程。本文将以另外一个例子为基础，在回顾Arithmetization过程的同时，将内容引申到多项式的LDT过程。

新的实例

AliceClaim：“我有1000,000个数，他们都在范围内”。为了方便验证者Bob验证，Alice首先要对Claim进行Arithmetization转换。过程如下图1所示(图中：黑色箭头代表主流程，红色箭头代表附加说明信息，黄色圈对应下面详细说明的索引)

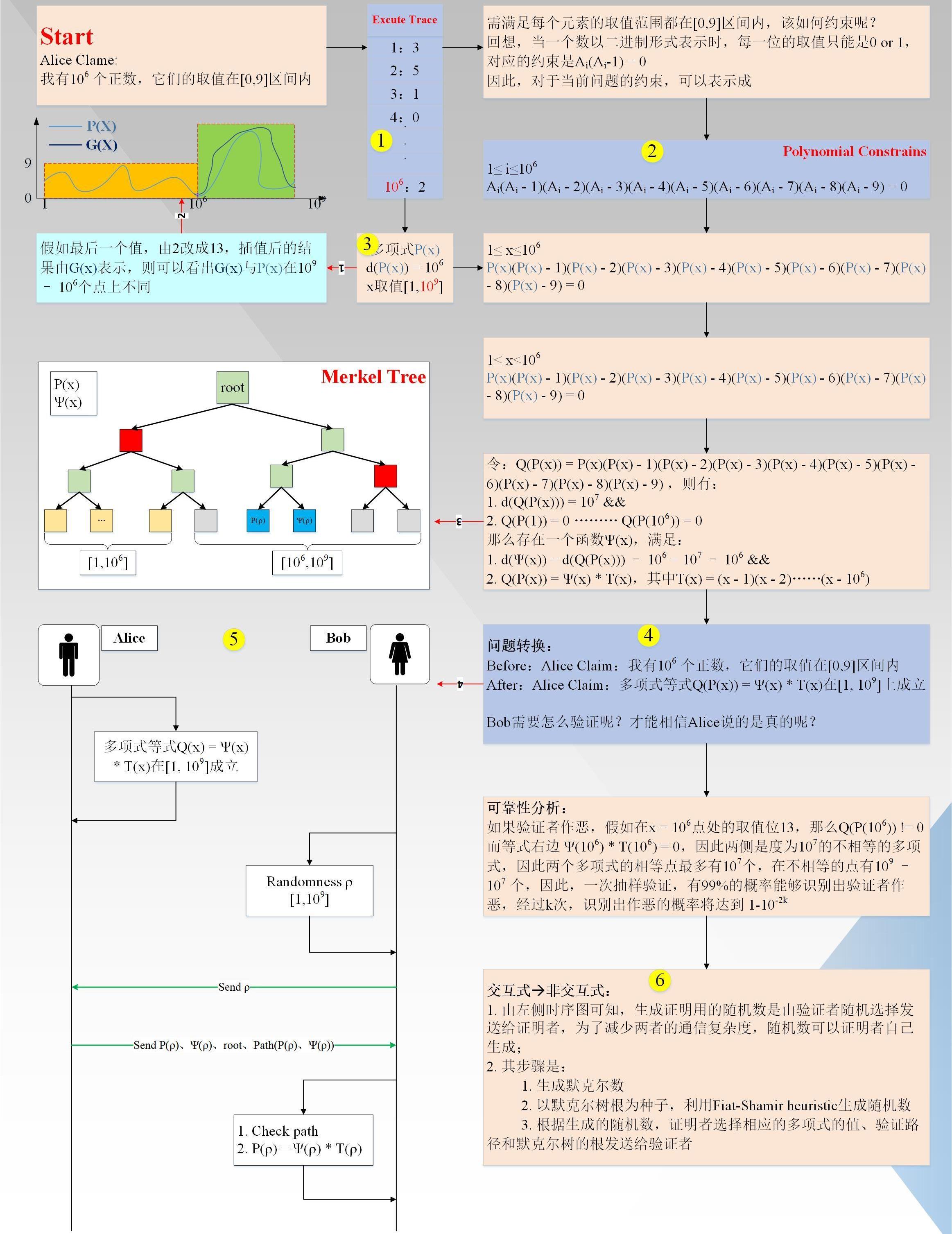
下面具体说明一下对应流程：

首先生成执行轨迹(EXCUTETRACE)，事实上，它是一张表，总共有1000,000行；

生成多项式约束(PolynomialConstrains)，多项式约束满足执行轨迹的每一行(个人理解：步骤1，2没有一定的先后依赖关系，只是习惯上先生成执行轨迹，再生成约束多项式)；

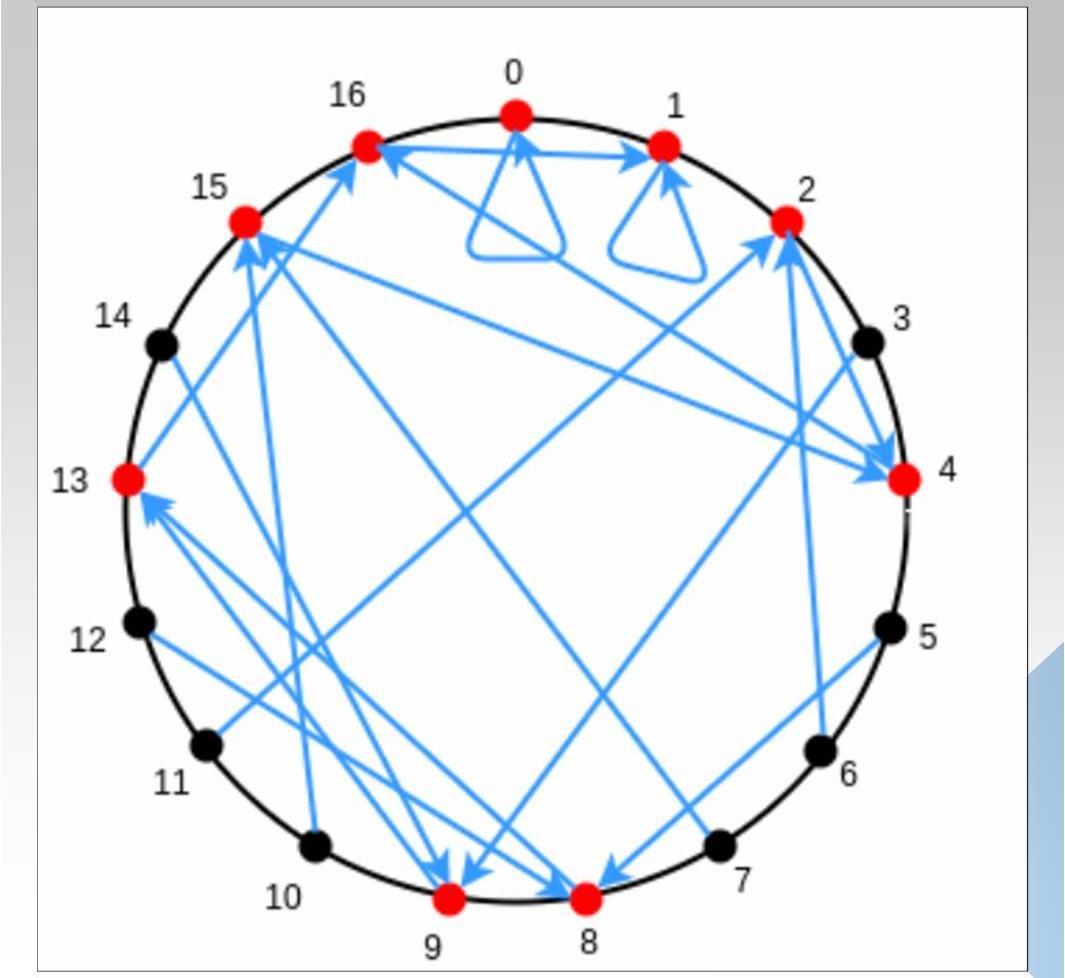
对执行轨迹进行插值，得到一个度小于1000,000的多项式P(x)、x取值，并计算更多点上的值，x取值范围扩大到(Reed-Solomen系统编码)；假如，证明者有一个值不在范围内(图中红线1/2所示)，假如就是第1000,000个点，它实际的值是13，大于9，其插值后的曲线G(x)如图所示，图中P(x)为有效曲线，G(x)为无效曲线。可以看出，两条曲线在变量x取值范围内，最多有1000,000个交点，即有1000,000,000-1000,000个点不同，这很重要。

将插值后的多项式P(x)和多项式约束进行组合变换，最终得到的形式为：

动态 | 应深刻了解区块链技术的利弊 使之服务于国防等关键领域:中国军网今日刊文称，区块链作为一个“去中心化”分布式账本数据库，其具有分布式去中心化、无须信任系统、数据不可篡改等优点。文中表示：若我们盲目地将其应用在国防及其他关键领域，其后果不容乐观。比如存储机制耗费资源，运行机制影响效率，共识机制存在安全隐患。面对区块链这一新兴事物，必须深刻了解其技术利弊，优化改进其不足，才能更好地驾驭该技术，使之服务于国防等关键领域。[2018/12/7]

Q(P(x))=Ψ(x)*T(x)，其中T(x)=(x-1)(x-2)……(x-1000,000)，x取值

其中，d(Q(P(x)))=10,000,000、d(Ψ(x))=10,000,000-1000,000、d(T(x))=1000,000；

至此，问题就转化成了，Alice宣称“多项式等式在变量x取值范围内成立”的问题。那么验证者Bob该如何验证呢？具体过程如下：

证明者Alice在本地计算多项式P(x)、Ψ(x)在所有点上的取值，对！从1至1000,000,000，并形成一个默克尔树；

验证者Bob随机的从内选取一个值ρ，并发送给证明者Alice，要求其返回对应的信息；

证明者Alice返回P(ρ)、Ψ(ρ)、root、AuthorizedPath(P(ρ)、Ψ(ρ))给验证者Bob；

验证者Bob首先根据默克尔树验证路径验证值P(ρ)、Ψ(ρ)的有效性，然后等式Q(P(ρ))=Ψ(ρ)*T(ρ)，如果成立，则验证通过；

完整性分析：如果验证者Alice是诚实的，那么等式Q(P(x))一定会被目标多项式T(x)整除，因此必定存在一个d(Ψ(x))=d(Q(P(x)))-d(T(x))的多项式Ψ(x)，满足Q(P(x))=Ψ(x)*T(x)，因此对于任意的x，取值在之间，等式都会成立；

动态 | 雄安新区采用区块链技术建立项目资金管理平台 打造植树造林的“雄安模式”:根据澎湃新闻消息，目前，雄安新区正应用区块链技术创新对造林资金进行监管。新区专门研发了采用基于区块链技术打造的项目资金管理平台系统，对植树造林参建单位及利益相关单位项目专项资金流向进行实时动态监控。在项目施工前，雄安集团就提前把所有参与植树工人的工资卡号收集好，关联到区块链平台系统，动态记录掌握工人的工作情况，造林的钱最终也直接打到每一个工人的账户上。雄安新区“千年秀林”工程创新体制机制，创造了植树造林的“雄安模式”：实行“投资人+施工总承包”模式，形成共建共享、充满活力、可持续造林机制，采用区块链技术创新监管造林资金，真正做到以人民为中心、共建共享森林发展。[2018/8/30]

可靠性分析：如果验证者Alice是不诚实的，即类似于步骤3里的假设，在x=1000,000上，P(x)的取值为13，那么Q(P(1000,000))!=0，但是等式右边，T(1000,000)=0，因此Q(P(x))!=Ψ(x)*T(x)，即等式两边是不相等的多项式，其交点最多有10,000,000个，因此通过一次随机选取，其验证通过的概率仅为10,000,000/1000,000,000=1/100=0.01，经过k次验证，其验证通过的概率仅是1-10(^-2k)；

上述的验证过程为交互式的，如果是非交互式的，可以利用Fiat-Shamirheuristic进行变换，以默克尔树的根作为随机源，生成要查询的随机点；

LDT

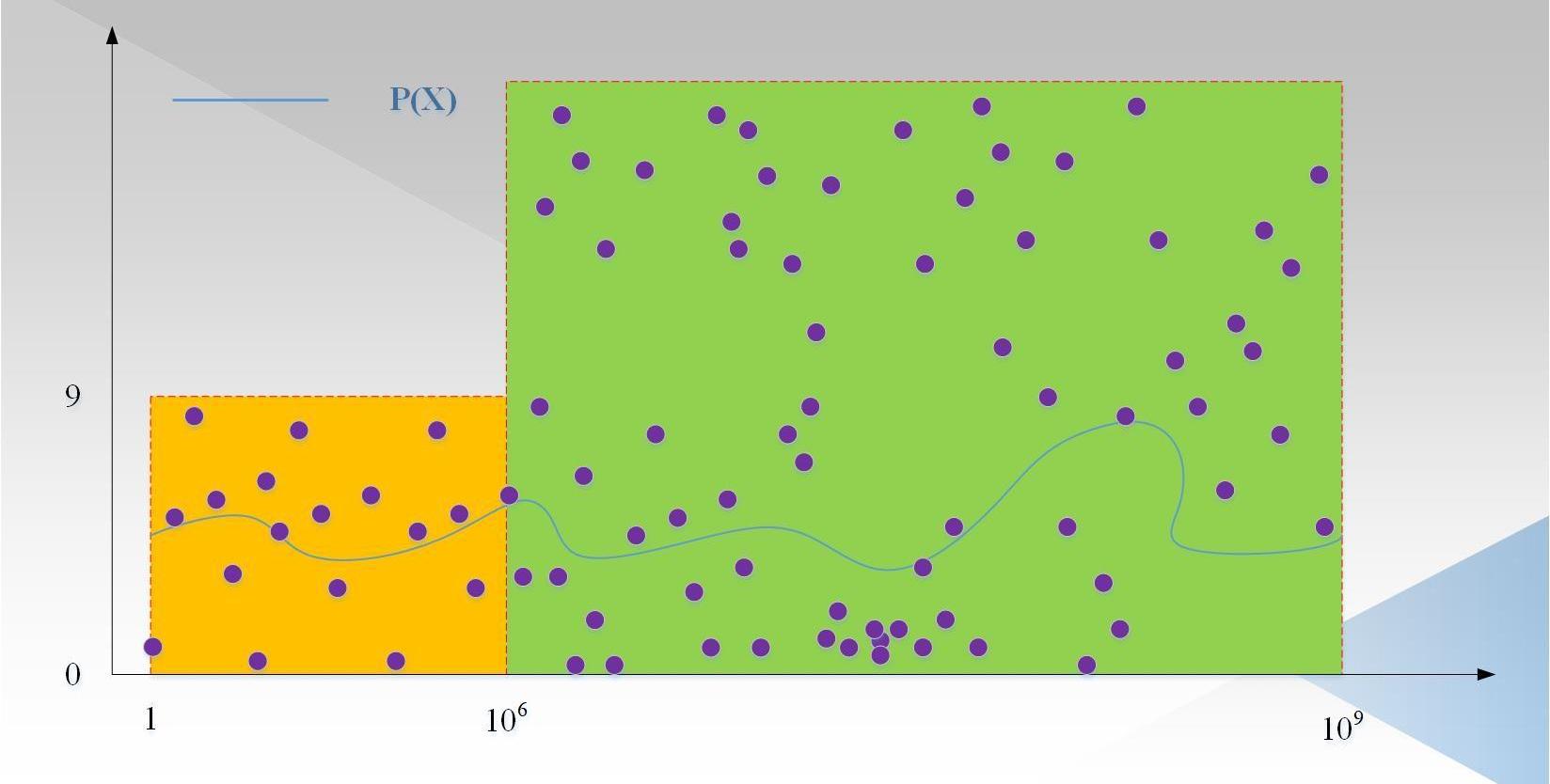
我们忽略了一种攻击方式，即针对每一个数x，证明者都随机生成p，然后根据Ψ(x)=Q(p)/T(x)，这些点不在任何一个度小于1000,000的多项式上，但是可以通过验证者验证。如下图2所示：

声音 | 河北副省长陈刚：加快运用区块链技术 打造高质量发展样板:8月5日消息，省委常委、副省长，雄安新区党工委书记、管委会主任陈刚强调：“要加快区块链、大数据等技术研究运用，把制度建设和信息技术相融合，不断扎紧监管制度的笼子，积极探索廉洁雄安建设的新路径。”[2018/8/5]

图中：紫色的点为随机生成的点p，这些点大概率不在一个度小于1000,000的多项式上(事实上，可以不考虑前1000,000个点，因为验证者只会从范围内取值)。因为即使选择1000,000个点插值出一个度小于1000,000的多项式，也不能保证其他的点在这个多项式上，因为其他的点是随机生成的。因此，需要有一种方式，保证证明者P(x)的度是小于1000,000，Ψ(x)的度小于10,000,000-1000,000。这就是LDT的目标，那LDT具体的过程是怎么样的呢？请继续往下看。

举个栗子，如果Alice想证明多项式f(x)的度是小于3的，即有可能是2次的或者是1次的。一般流程如下：

验证者Bob随机选取三个值a,b,c，发送给证明者Alice；

证明者Alice返回f(a),f(b),f(c)；

验证者Bob插值出度小于3的多项式g(x)，然后再随机选取一个点d，发送给证明者；

证明者Alice返回f(d)；

验证者Bob比对f(d)和g(d)的值，如果相等，则证明成立。

回归到一般情况，其过程可以用下图3表示：

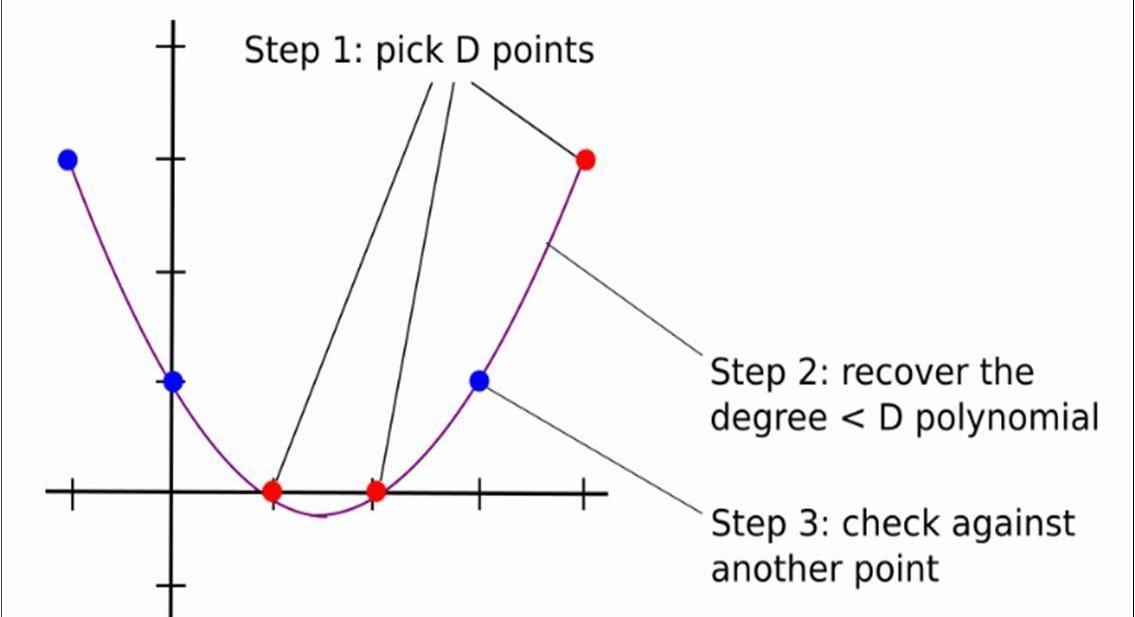
可以看出，如果D很大，Alice和Bob交互的次数则为D+k次，复杂度很高；有没有一种办法，使得两者之间交互的次数小于D的情况下，使得验证者相信多项式的度是小于D的，直接返回小于D个点肯定是不行的，因为那不能唯一确定一个度小于D的多项式，因此需要证明者需要额外发送一些辅助信息。下面我们以P(x)为例，详细阐述这个过程(事实上，应该是证明P(x)和Ψ(x)的线性组合小于10,000,000-1000,000，本文重点是LDT，因此只以P(x)为例，这并不影响对LDT的理解)。

金色财经现场报道 创大资本董事长许洪波：娱乐业最需要通过区块链技术得到改变:金色财经现场报道，在2018全球区块链精英峰会上，创大资本董事长 全球移动Java标准起草人许洪波进行以《用区块链重新定义娱乐产业打造面向全球的娱乐生态》为题的现场演讲，他指出：最需要通过区块链技术得到改变的是娱乐业。娱乐业产业存在诸如低效的中介环节、作者权益得不到保障、粉丝权益无法保障等痛点问题。区块链会从以下几方面重新定义创意产业：首先，区块链将改变生产关系，粉丝不仅是消费者，同时是明星的经纪人，可以极大提高娱乐产业产品的流通效率；其次，完整权益保护，通过智能合约对作品的流通进行追溯和确权，实现权益分配透明化；再次，创造数字收藏品的新兴产业，区块链保证了数码艺术的全球唯一性、永续性，具有易于交易等特征，是IP变现新蓝海。[2018/4/28]

假如P(x)=x+x^999+x^1001+x^999999=x+x^999+x*x^1000+x^999*(x^1000)^999;

此时，我们找到一个二维多项式G(x,y)，取值范围分别是、，满足：

G(x,y)=x+x^999+x*y+x^999*y^999可以发现，当y=x^1000时，满足：

G(x,y)=G(x,x^1000)=x+x^999+x*x^1000+x999*(x^1000)^999=P(x)

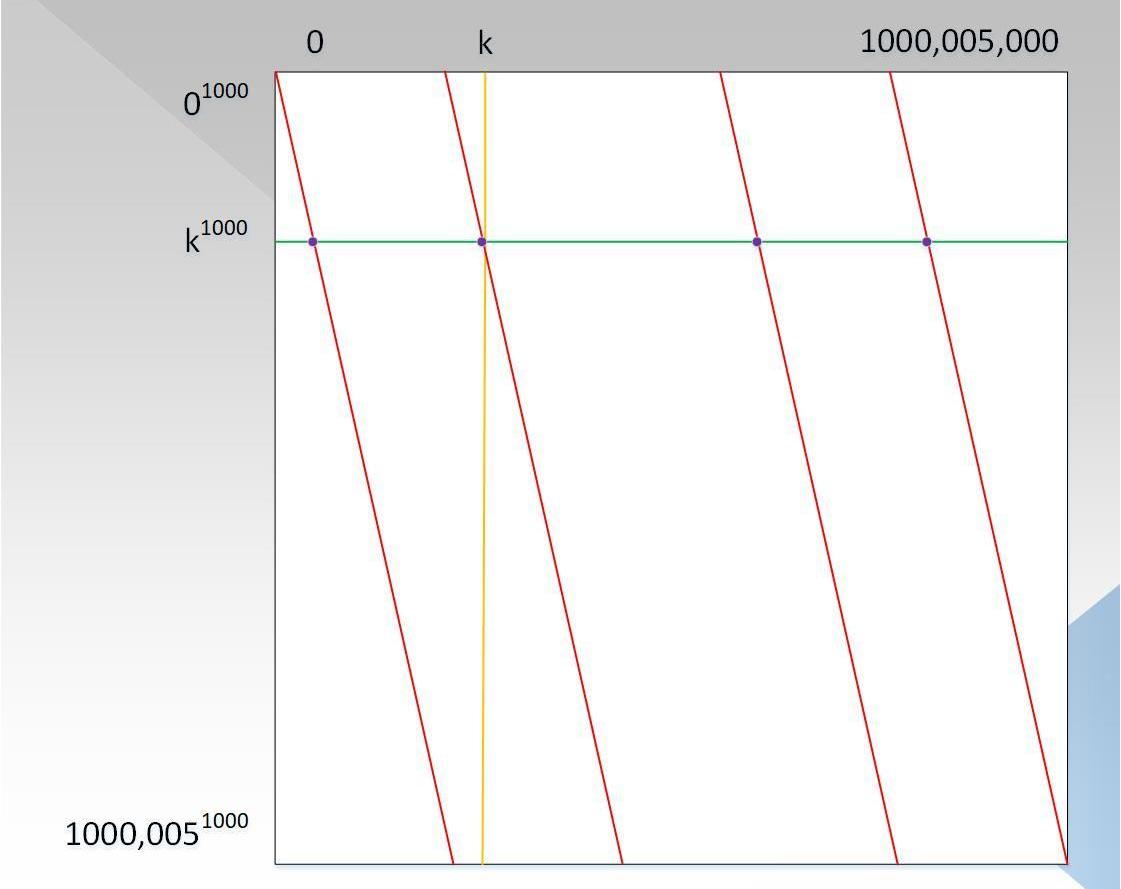
如果我们能证明G(x,y)相对的x,y的最高度都是小于1000，因为P(x)=G(x,x^1000)上，因此可以相信P(x)的度小于1000,000；如图4所示：

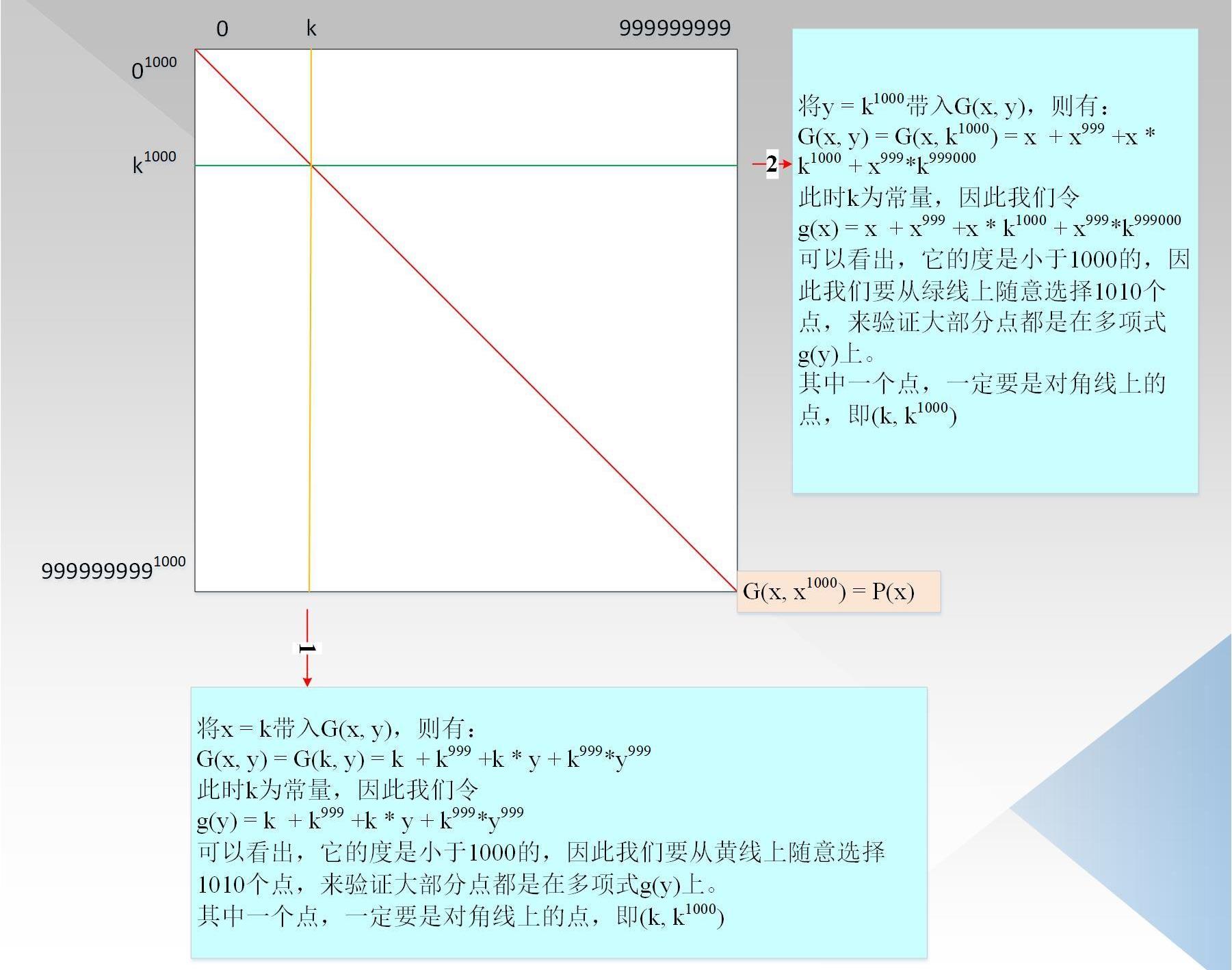
验证者把所有的点都计算好，形成一颗默克尔树。验证者随机选择一行和一列，如图中红线1/2所示，对于每一列，它是由关于y的度小于1000的多项式生成，对于每一行，它是由关于x的度小于1000的多项式生成。验证者从行/列中随机选择1010个点，用来验证对应行/列上的点是否在度小于1000的多项式上，需要注意的是，因为P(x)的点都在上图的对角线上，因此我们要确保每一行/列对应的对角线上的点也在对应的度小于1000的多项式上，即1010个里面一定要包含对角线的点。

丹华资本张首晟：看好区块链技术 呼吁大家关注欧洲区块链的发展:丹华资本创始人、美图独立董事张首晟表示，看好区块链技术，丹华资本非常关注区块链，也投资了多家区块链项目。对于中美区块链项目发展的差异，张首晟表示，两边都做得很好，他强调，大家也要多关注欧洲区块链的发展。[2018/3/25]

可靠性分析：如果原始多项式的度实际上是小于10^6+10999，即P(x)=x+x^999+x^1001+x^1010999，那么对应的G(x,y)为G(x,y)=x+x^999+x*y+x^999*y^1010，即，对于每一个x，G(x,y)是关于y的一元多项式函数，且度d<1010，因此下图中的每一列所有点都是在度d<1010的多项式上，而不在d<1000的多项式式上。所以如果证明者任然宣称多项式P(x)的度d<1000,000，则会验证失败，其他场景是同样的道理

那有没有可能恶意证明者仍以G(x,y)=x+x^999+x*y+x^999*y^999的形式去生成证据呢？这样会验证通过吗？

我们知道，我们在验证时着重强调了对角线上的那一点一定要在多项式上，我们知道，此时对角线对应的多项式形式是

P(x)=x+x^999+x1001+x^999999，而实际的P(x)，我们在这里标记为P`(x)，其形式是：

P`(x)=x+x^999+x^1001+x^1010999

因此，如果验证者恰好选择的点是两个多项式的交点，则会验证通过，事实上，两个多项式最多有1000,000左右个交点，但是由于随机选取的点不是证明者自己选取，是由默克尔树的根为种子随机生成，因此证明者没有机会作恶，去可以选取那些能通过验证的点。

由于总共由10^9个点，因此随机选取一个点，能验证成功的概率为10^6/10^9=10^(-3)，如果选择k行，则成功的概率仅为10^(-3k)。

以上可以看出，验证者和证明者只需要交互1010*2*k个点，就可以完成验证，假如k=10，则1010*2*10=20100<<10^6。

虽然上述实现了在交互次数小于D的情况下，完整LDT验证，但是证明者的复杂度过于庞大，至少10^18的复杂度远远大于原始的计算，因此需要一些优化方案，降低复杂度。话不多说，直接引入有限域，毕竟在实际项目中，我们可不希望数值本身过于庞大。直接引用费马小定理的结论：在有限域p内，如果满足(p-1)能被k整除，则映射x=>x^k的像只有(p-1)/k+1个。下图5以p=17，映射x=>x^2为例：

图中，红色为x^2在有限域p内的象，总共由(p-1)/2+1=9个。同时我们可以发现，9^2和8^2的像一致，10^2和7^2的像一致，以此类推，16^2和1^2的像一致，记住这个现象，对下一张图的理解有帮助。

因此，在本例中，我们选择一个素数p=1000,005,001，其满足：

为素数

p-1能被1000整除

p要大于10^9

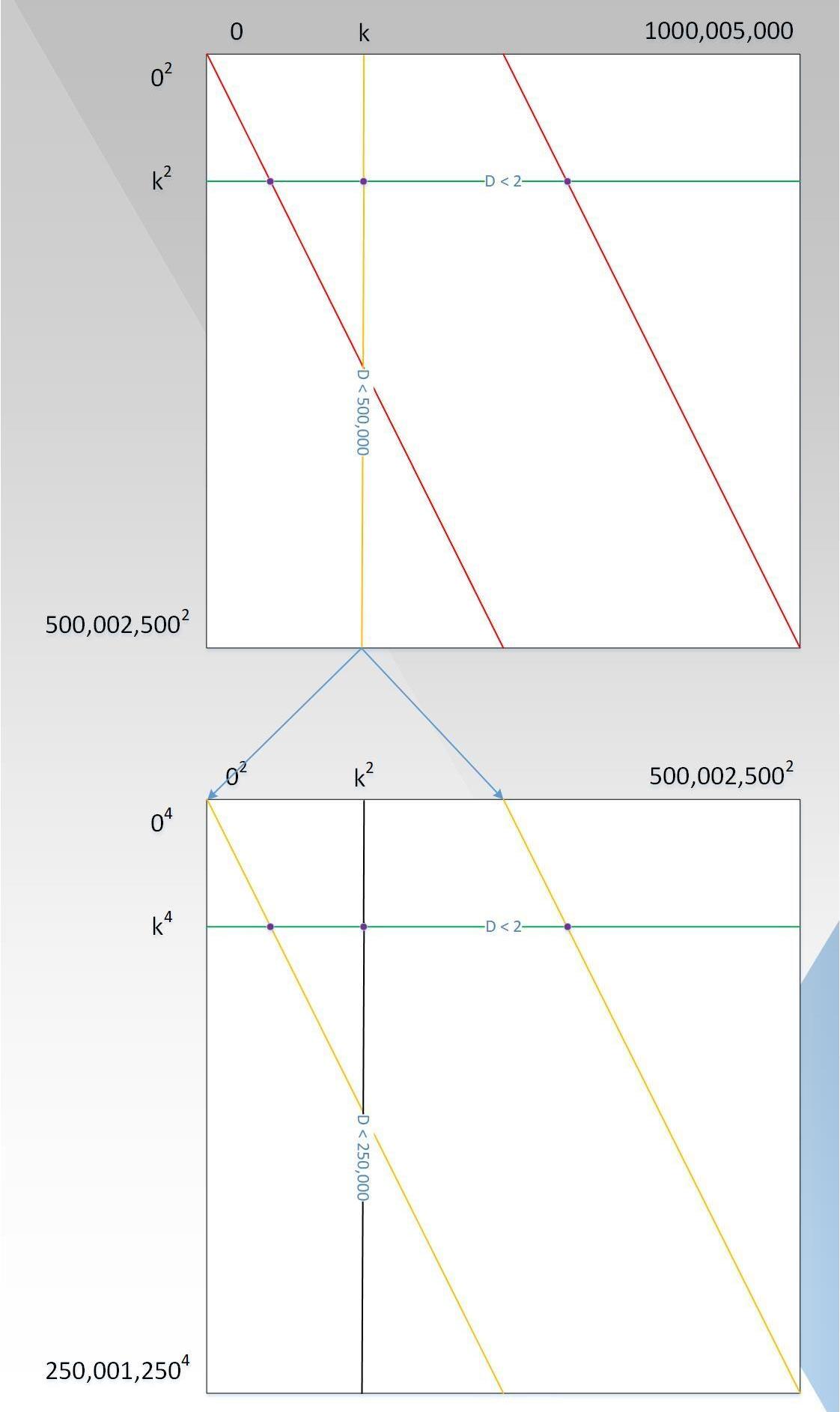
因此，在有限域p内，x=>x^1000的像在p内有(p-1)/1000=1000,005个，因此图4可以变成图6的形式：

可以看出，列坐标变成了10^6个元素，对角线变成了平行的线条，总共有1000个。还记得上面费马小定理结论的特殊现象吗？这就是对角线这种分布的原因，读者试着去理解(可能读者会觉得，对角线应该是锯齿形，不是这种平行的形式，也许你是对的，但是这并不影响验证流程)。此时证明者的复杂度已经从10^18减少到了10^15次方，证明和验证过程和步骤3描述的仍然一致。

还能不能继续优化呢？答案是肯定的。回想起前面所述的验证过程，对于每一行/列，验证者都要获取1000个点进行插值得出一个度小于1000的多项式，仔细观察图6，对于每一行，原始数据里不就是有1000个数么？那我们干脆选这些点插值出一个度小于1000的多项式，然后只需要随机让证明者再计算任何一列，并且证明沿着列上的点都在度小于1000的多项式上，并且列上的点也在对应的利用原始数据插值出的行多项式上。此时，证明者复杂度从10^15减少到了10^9次方。

总结：个人理解，从步骤1到步骤5，其实是PCP到IOP的选择过程。

PCP要求证明者生成全部的证据，然后验证者多次随机选取其中的某一部分进行验证，但是这样，证明者的复杂度仍然很高；

IOP要求证明者不用生成全部的证据，根据多次的交互，每次生成只需生成部分证据，使得证明的复杂度和D呈近似线性关系；

证明者复杂度已经降低到了与D呈拟线性关系，验证者的复杂度虽然是亚线性，交互次数已经低于D，但是能不能优化到更低呢？基于证明复杂度的最优设置，我们继续探索验证复杂度的优化之路，回顾P(x)=x+x^999+x^1001+x^999999=x+x*(x^2)^499+x*(x^2)^500+x*(x^2)*499999，令G(x,y)=x+x*y^499+x*y^500+x*y^499999，则当y=x^2时，有G(x,y)=G(x,x^2)=x+x*(x^2)^499+x*(x^2)^500+x*(x^2)*499999=P(x)。最终的图应如下图7所示：

从图中可知：

证明则复杂度仍为10^9次方；

每一行上的点都在度d<2的多项式上，因为当y取固定值时，G(x,y)就是关于x的一次多项式；

每一列上的点都在度d<D/2的多项式上，证明者需要证明这个多项式是小于D/2的，假定这个多项式为P1(x)，这个时候，并非验证者选取大于D/2个点去验证，因为验证复杂度仍然不够低，而是对这一列再一次用到类似于P(x)的处理过程，如图7中下面的图所示，以此循环，直到可以直接判断列上的多项式的度为止，类似于行。

总结

至此，本篇文章就结束了，总结下来，本文主要阐述了以下几个内容：

如何转换问题形式--Arithmetization

为何需要LDT--为了验证简洁

LDT的大概过程--二分法验证，类似于FFT

降低LDT的复杂度--有限域+IOP

至于LDT的详细过程，将留给本系列的最后一篇，敬请关注。

谢谢大家，欢迎批评指正，有任何问题或者疑问可以留言。

标签：区块链ALIICELIC区块链是局吗Centralityalice币最新消息blockchainresearchandapplication

fil币价格今日行情热门资讯