比特币:探讨 | 比特币的醉汉价值：价值预测模型S2F是否是虚假的假设？_FLO

前言：S2F是用来对比特币价值进行预测的模型。那么，S2F是否是虚假的假设？本文则试图对此进行证伪，最后它的结论是：“比特币就像是醉汉，而Stock-to-Flow就是回家的路。”本文作者是Nick，由蓝狐笔记“HQ”翻译。

摘要

本文将探讨比特币的价值是否存在stock-to-flow的关系。对所提出的对数模型的统计有效性、各变量的平稳性以及潜在的虚假关系都进行了检验。建立了一个向量误差修正模型，并与stock-to-flow模型进行了比较。

尽管这些模型中，有些在Akaike信息标准方面超过了原始模型，但它们都未能对stock-to-flow是比特币价值的一个重要非虚假预测因素的假设进行否定。比率模型是指可用资产或储备资产的数量除以每年生产的数量，Stock-to-Flow比率是一个重要的指标，因为S2F中较高的指标值反映了资产每年通货膨胀发生率的降低。）

注意

·?所有分析均使用Stata14完成

·?不构成投资建议

简介

科学方法对大多数人来说是难以理解的，毕竟这是反直觉的。它的最终结论可能不反映个人信仰。这个方法需要一个基础来理解这个基本概念：存在错误是允许的。这应该是学校里教的东西。如果我们害怕出错，就永远不会提出新的建议。

因此，科学发现的历史，是由其“机缘巧合的本质”所决定的。人们偶然发现的事情，可能和他们最初打算做的事情一样重要。他们最初的想法也许是不正确的、或没有定论的，但他们在探索的过程中发现的东西为后继者建立了框架。

根据伟大的现代科学哲学家卡尔·波普尔的说法，检验一个假设是否存在错误的结果，是唯一可靠的方法，可以为论证它是正确的论点增加份量。

如果严格而重复的检验不能证明一个假设是错误的，那么每次检验假设一个更高的可能性是正确的。这个概念叫做可证伪性。本文旨在对比特币价值的stock-to-flow模型进行证伪，该模型是在“比特币价值稀缺性模型”中被定义的。

对问题进行定义

要证伪一个假设，首先我们必须说明它是什么：

零假设：比特币的价值是比特币stock-to-flow的函数

备选假设：比特币的价值不是比特币stock-to-flow的函数

S2F模型的作者通过在比特币市值的自然对数和stock-to-flow的自然对数上拟合一个普通最小二乘回归来检验H0。对于这两个变量中的对数转换，除了对数模型可以用幂律表示外，没有其他的方法或任何已知的推理可以表示。

该模型没有考虑由于非平稳性而产生虚假关系的可能。

方法

在本文中，我们将使用正态回归探索该模型，并确定对数转换是否必要、或是否适当，并探索可能的混淆变量、交互作用和敏感性。

美参议院银行委员会召开加密货币听证会，探讨加密货币是否波及金融体系:美国参议院银行委员周二召开了一场名为“加密货币有什么好处？”的听证会，除几位议员展现积极态度外，多数议员仍有疑虑。他们主要关心两个问题：加密货币去中心化的本质到底如何，以及加密市场的系统风险会不会波及传统金融体系。参与听证会的圣玛丽大学法学院教授Angela Walch表示：通过现实镜头审视加密货币，可以看出，它并非一张神奇的脱离金融系统的自由卡。我们要承认其中的权力集中问题，并制定深思熟虑的应对政策和风险决策。Walch认为不能对加密系统集中的“权力口袋”视而不见，包括核心软件开发人员和矿工可利用他们的权力地位，对系统用户施加影响。民主党参议员Elizabeth Warren表示：金融系统受到一些在暗中不露面的超级程序员和矿工的影响。Warren还在周二去信财长耶伦，呼吁联邦机构统一制定针对加密货币的监管框架。她在信中写道：”随着对加密货币的需求不断增长，这些资产越来越深地嵌入我们的金融体系，消费者、环境及金融体系正面临越来越大的威胁。”研究和倡导组织Coin Center的执行董事Jerry Brito表示，虽然加密货币发展中的问题可能对传统金融系统造成风险，但美国不应回避加密货币，而应为对冲基金和其他市场参与方设置护栏。他认为加密货币终究是一种大宗商品，任何大宗商品都会带来类似威胁。展现积极态度的参议员包括共和党参议员Cynthia Lummis，他称开源金融的透明度和开放性有助于促进金融包容性。民主党参议员Sherrod Brown则称区块链技术也有许多有用的非金融应用。（CNBC）[2021/7/28 1:19:40]

另一个有待探讨的问题是非平稳性。平稳性是大多数统计模型的假设。这是一个在任何时刻都没有趋势的概念，例如，对时间来说，平均值是没有趋势的。

在进行平稳性分析之后，我们将探讨协整的可能性。

符号说明

可用的数学符号是相对有限的。估计统计参数的常用符号是在顶部加一顶帽子。相反，我们将估计定义为。例如β的估计值=。如果我们表示的是一个4x4矩阵，我们将用表示等。下标项用@-eg表示，比如向量X中的第10个位置，我们通常用10下标X，即X@10。

普通最小二乘法

普通最小二乘回归，是一种估计两个或多个变量之间线性关系的方法。

首先，定义一个线性模型，它是X的某个函数Y，但有一些误差。

Y=βX+ε

其中Y是因变量，X是自变量，ε是误差项，β是X的乘数。OLS的目标是估计β，并使ε最小化。

为了使成为可靠的估计数，必须满足一些基本假设：

1.?因变量和自变量之间存在线性关系

2.?误差是同质的

3.?误差正态分布，平均值为零

4.?误差不存在自相关

线性

美国国会探讨远程投票概念 并讨论区块链投票利弊:美国国会目前正在努力应对在新冠病疫情期间于华盛顿重新召开会议的风险。4月30日的一份参议院工作人员备忘录显示，美国国会探讨了远程投票的概念，以及它所涉及的技术和法律考虑；其中，备忘录的一部分讨论了使用区块链投票的利弊。备忘录中提到，区块链通过其加密的分布式分类账，既可以安全地传输选票，又可以验证正确的选票。这些特性使得区块链在电子投票中非常有用。区块链可以为交易提供一个安全和透明的环境，并提供所有选票的无篡改电子记录。它还降低了不正确计票的风险。不过备忘录本身并没有公开支持使用该技术，也讨论了列部署该技术所涉及的潜在风险。(The Block)[2020/5/4]

我们首先看看市值与stock-to-flow之比的非转换散点图

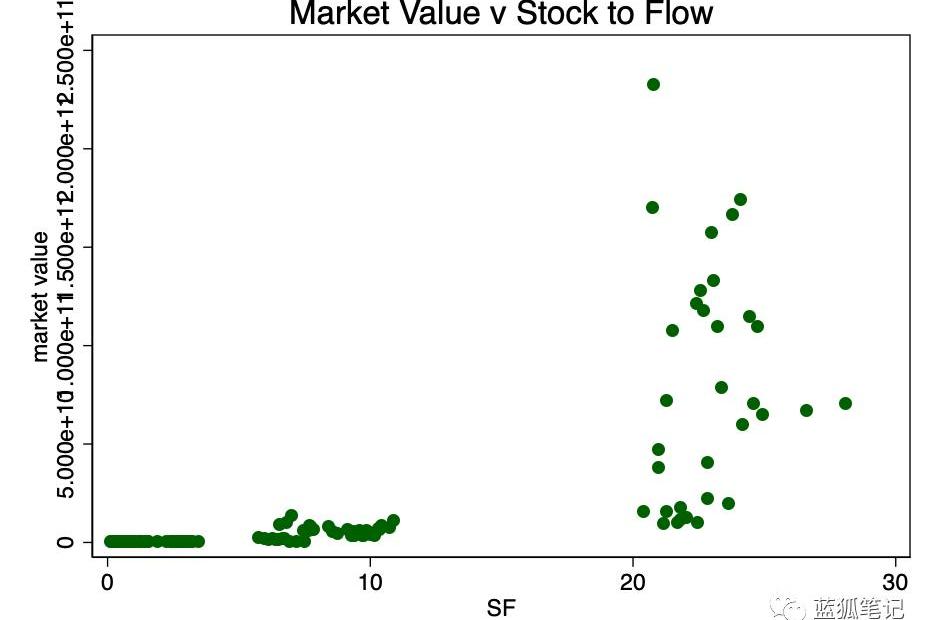
图1-市值与stocktoflow之比。数据太稀疏，无法确定关系。

在图1中，我们有了一个很好的理由来使用市场价值的对数——因为跨度太大了。取市场价值的对数并重新绘制，可以得到一个我们非常熟悉的对数图模式。

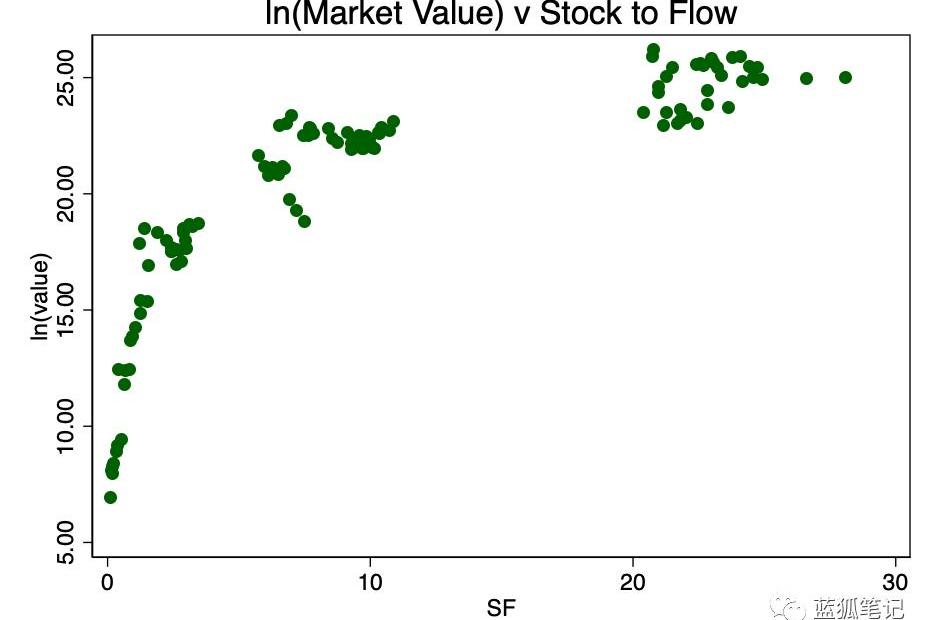
图2-市值对数与SF之比。一个清晰的对数模式出现了。

取stock-to-flow的对数并再次绘制，我们得到了图3，存在明显的线性模式。

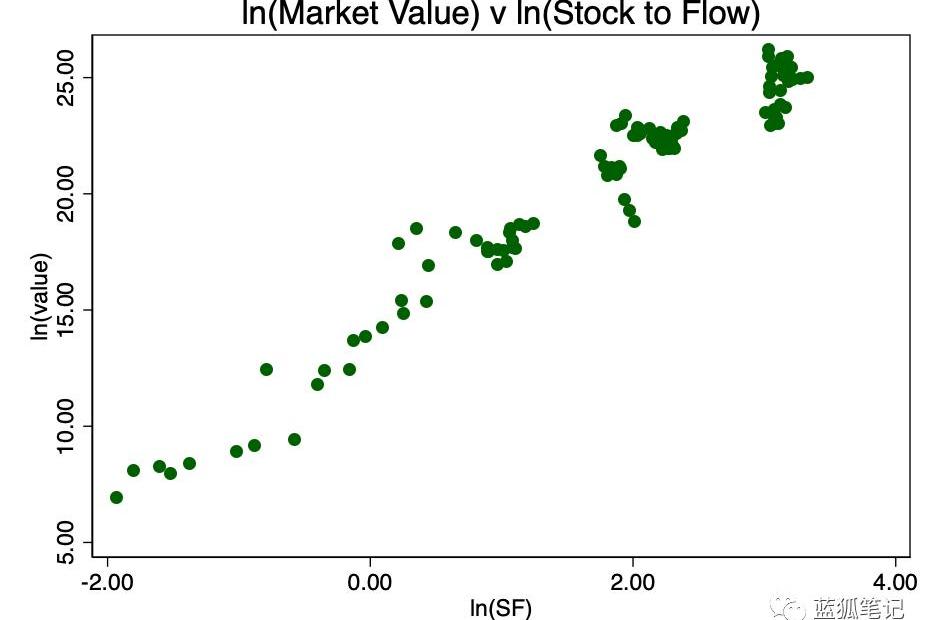
图3-出现了明显的线性关系

这证明了“对数-对数”的这种转换是唯一真正能显示良好线性关系的方法。

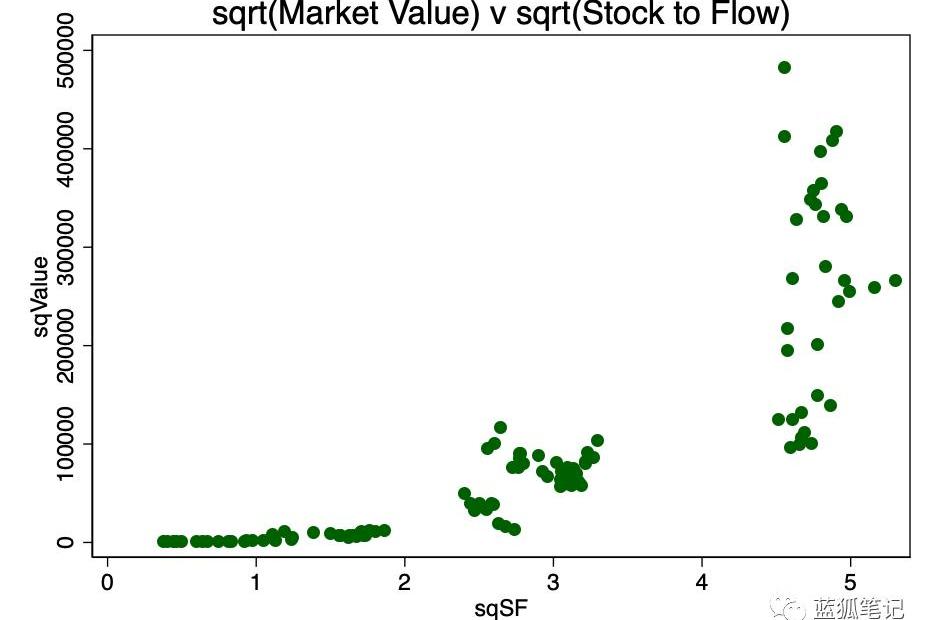
另一种转换是取两者的平方根。这个模式如图4所示。

浩云科技：公司与广州大学合作探讨区块链在金融物联等领域应用:浩云科技（300448.SZ）在互动平台回答投资者提问时表示，公司与广州大学共建公共安全智能实验室，探讨区块链技术在智慧司法、金融物联等业务领域的应用。[2020/3/21]

图4-平方根转换

显然，对数变换最适合满足第一个假设的要求。

因此，初步分析不能拒绝H0。

下图5展示了对数拟合回归的结果，其中=

图5-对数回归结果

使用该模型，我们现在可以估计残差和拟合值，并检验其他假设。

同方差性

如果误差项中的恒定方差的假设是真的，那么误差项的预测值中的每一个值，都会随机地在0左右移动。因此，使用RVF图是一种简单有效的图形方法，来确定这一假设的准确性。在图6中，我们看到的是一个模式的一小点，而不是随机散射，这表示误差项的一个非恒定方差。

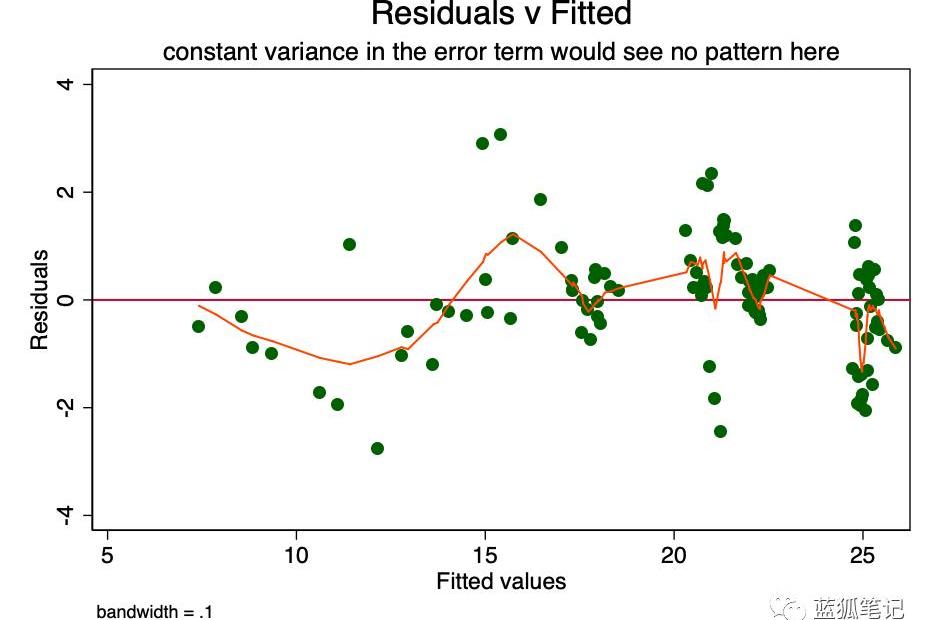
图6-RVF图。这个图的走势表示可能存在问题。

这样的异方差性，会导致系数的估计值具有更大的方差，因此不太精确，并且导致p值比它们原本的更加显著，因为OLS程序没有检测到增加的方差。因此，当我们计算t值和F值的时候，我们对方差进行低估，从而得到更高的显著性。这也对?的95%置信区间产生影响，β本身是方差的函数。

在这个阶段，继续使用回归来理解这些问题的存在是合适的。我们可以用别的一些方法来处理这些问题-例如，自举法、或方差的鲁棒性估计值。

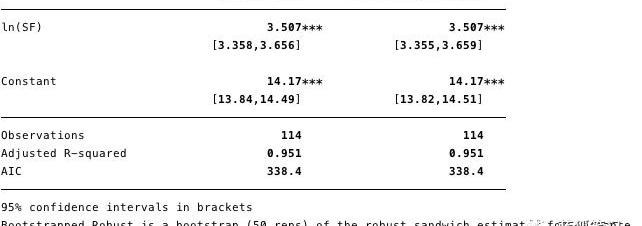
图7-异方差的影响，鲁棒性估计所示

如图7所示，虽然方差小幅增加，但在很大程度上，异方差并不会有那么大的不利影响。

在这个阶段，我们不能因为异方差而拒绝H0。

动态 | Konrad S. Graf 发文探讨比特币稀缺性和治理方式蕴含的价值:比特币货币理论研究者 Konrad S. Graf发表了最新的论文，进一步探讨了比特币的区块大小限制、人为制造的稀缺性和以代码增强的公共俱乐部治理方式（Code-Enhanced Public Club Governance）。Konrad S. Graf在推特上表示，这个话题已经困扰了我约6年的时间了。在论文中，作者将基于奥地利学派的行动理论方法从经济和法律的角度进行解释，并包含了这些概念：1. 包含交易的市场与非市场在在验证和接力服务中的区别；2. 自愿稀缺性与自然稀缺性、强制稀缺性的不同；3. 通过代码增强的公共俱乐部治理方式；4. 将进化模型运用于意识形态取向，主要对比了避免硬分叉和拥抱硬分叉的区别。Konrad S. Graf 之前还发表过一些关于比特币货币理论的论文，包括《比特币可以拥有吗？产权，知识产权错误和法律理论的意义》和《比特币的起源：货币演变的阶段》等。[2019/12/26]

误差的正态性

误差项的正态分布且平均值为零的假设，比线性或齐次性的假设更不重要。非偏态残差的非正态性，会使置信区间过于乐观。如果残差有偏差，那么你的结果可能会有一点偏差。然而，从图8和图9可以看出，残差有足够的正态性。平均值表面上为零，虽然正式测试可能会拒绝正态性的假设，但它们与正态曲线的拟合程度足以使置信区间不受影响。

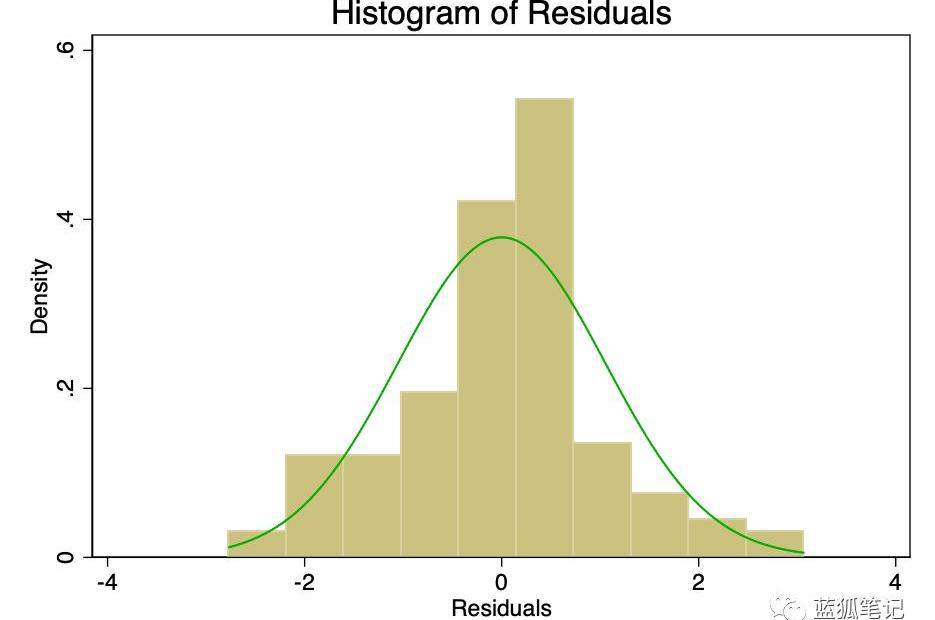
图8-覆盖正态分布的误差项直方图。

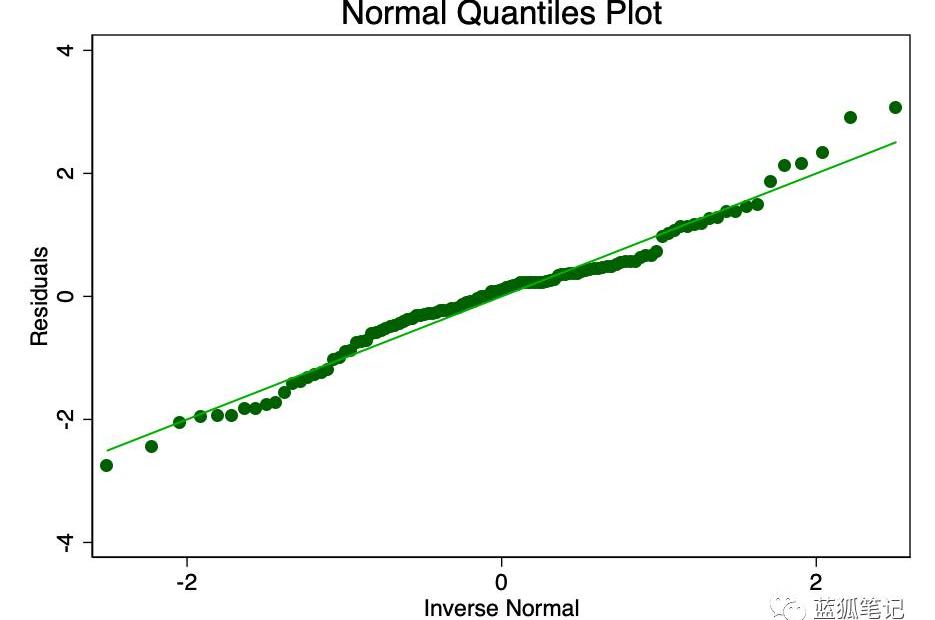
图9——误差项的正态分位数图。圆点离直线越近，正常拟合效果越好。

杠杆

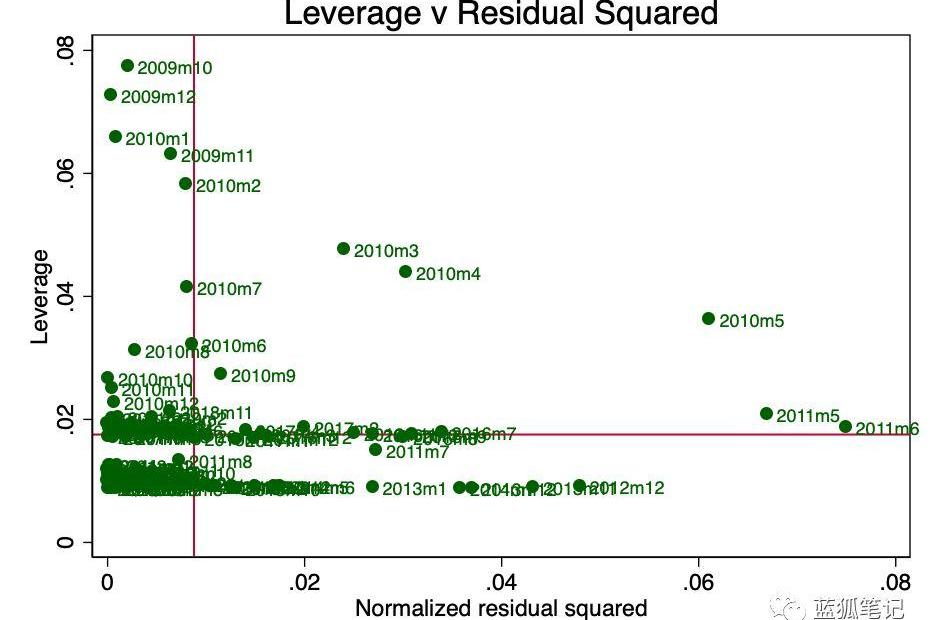
杠杆是这样一个概念：回归中并非所有数据点对系数的估计都有同等的贡献。一些高杠杆率的点可能会显著地改变系数，这取决于它们是否存在。在图10中，我们可以很清楚地看到，从早期开始，出现了一些令人担忧的问题。这一点也不奇怪，S2F的作者在前面说过，收集早期的价值存在一些问题。

全国政协委员王鹏杰：探讨建立国家层面的区块链数字资产交易平台:全国政协委员王鹏杰提出开展区块链数字资产项目“核准制”监管，推行个人区块链账户“实名制”认证，做好区块链数字资产投资者的教育工作等建议。此外“还要探索建立国家层面的区块链数字资产交易平台。”王鹏杰建议在健全国内相关法律法规后，在央行和证监会等部门的统一协作下，成立受监管的、高效廉洁的区块链数字资产交易平台，为企业募资和投资者资产增值提供正规渠道。[2018/3/3]

图10-杠杆与残差平方之比

如果我们在没有这些点的情况下进行重新回归，并且由于我们知道存在异方差问题，那么我们应该使用鲁棒性估计值。

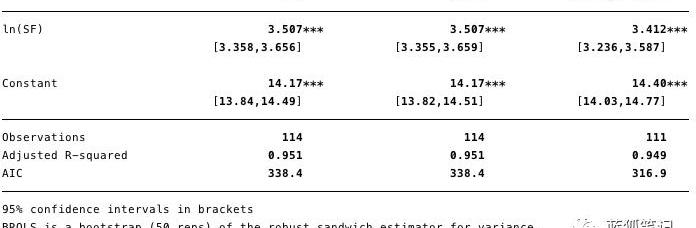
图11-去除高杠杆的点，实质上是改变对的估计，并改进了赤池信息准则。

在图11中，我们可以看到，通过去掉这三个点后，的估计值大不相同，赤池信息准则也大不相同，这表明尽管R2较低，但这是一个更好的模型。

OLS结论

基本诊断表明：原始OLS中存在一些小的可修复的问题。现阶段我们不能拒绝H0。

平稳性

平稳过程被称为0阶积分。非平稳过程是I(1)或更多。在这种情况下，整合更像是“可怜”的——它是滞后差异的总和。I(1)意味着如果我们从序列中的每个值减去第一个滞后值，我们将有一个I(0)的过程。众所周知，非平稳时间序列上的回归是可以识别出虚假关系的。

在下面的图12和13中，我们可以看到我们不能拒绝ADF检验的零假设。ADF检验的零假设是指数据是非平稳的。也就是说，我们不能说数据是平稳的。

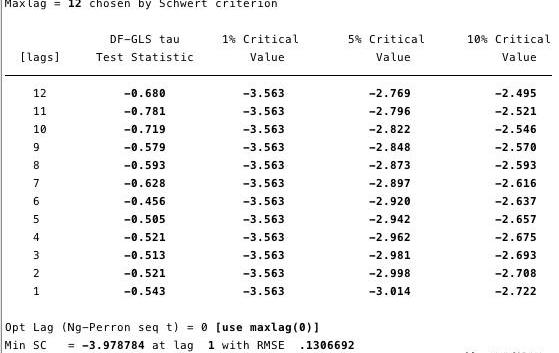
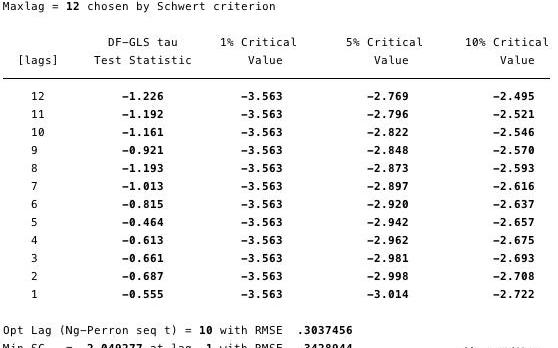
图12和13——对ln(市值)?和ln(SF)?单位根的GLSADF检验。

KPSS检验是ADF检验平稳性的补充检验。这个检验有一个零假设，即数据是平稳的。如图14和15所示，我们可以拒绝两个变量中大多数滞后的平稳性。

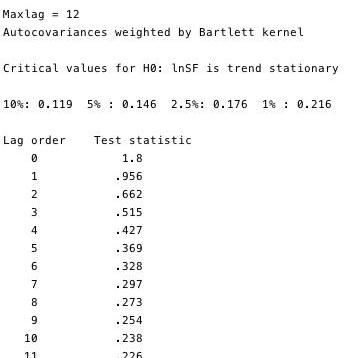
图14和15-针对零平稳性的KPSS检验

这些检验证明了这两个序列毫无疑问是非平稳的。但这有点问题，如果这个序列不是趋势平稳的，那么OLS可能会被误导去发现一个虚假关系。我们可以做的一件事情是：取每个变量的对数月差，然后重新做OLS。然而，由于这一问题在计量经济学中普遍存在，我们有一个更具有鲁棒性的框架——即所谓的协整。

协整

协整是一种处理一对I(1)过程、并确定是否存在关系、以及该关系是什么的方法。为了理解协整，我们举一个简单例子——醉汉和他的狗。想象一个醉汉用皮带牵着他的狗回家，醉汉毫无方向地走来走去。狗走路也是相当随机：嗅树，吠叫，追逐抓挠一只小狗等等。

不过，狗的整体方向会在酒鬼的皮带长度的范围内。因此我们可以估计，在醉汉回家路上的任何一点上，狗都将在醉汉的皮带长度内。这种简化类比的就是一个粗略的协整——狗和主人一起移动。

不同于相关性，假设一只流浪狗，在回家路上95%的时间都跟着醉汉的狗在走，然后跑去追一辆车到了镇子的另一边。流浪狗和醉汉之间的路径有着很强的关联性，不管醉汉曾经有过多少个在外面晃荡的夜晚，这种关系并不意味着什么，也不能用来预测醉汉将会在哪里，在过程中的某些部分，它是真的，而在另外一些部分，它是非常不准确的。

为了找到醉汉，首先，我们将看到我们的模型应该使用什么样的滞后顺序规范。

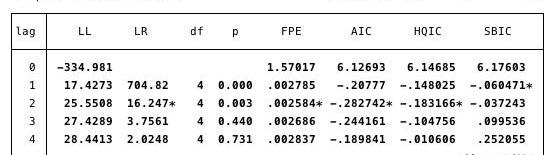
图16-滞后顺序规范。用于确定AIC最小值。

我们在这里确定了：最合适的滞后规范是2阶AIC最小值。

接下来，我们需要确定是否存在协整关系，Johansen框架是很好的工具。

图17-Johansens协整测试

图17的结果，说明lnvalue和lnSF之间至少存在一个协整。

我们将VECM定义为：

Δy@t=αβ`y@t-1+Σ(Γ@iΔy@t-1)+v+δt+ε@t

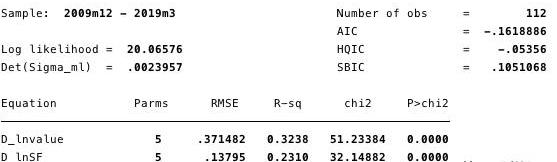
图18-关于整体模型方程的信息

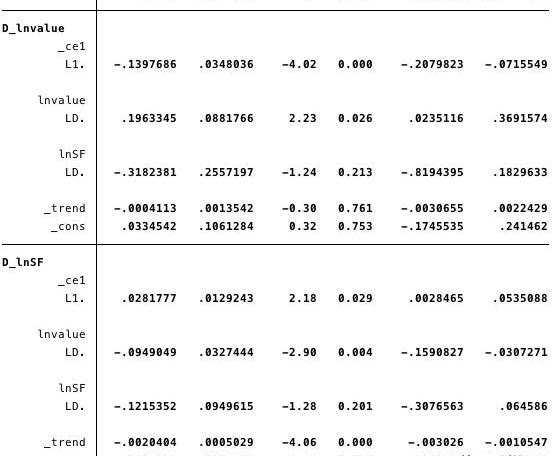
图19-短期参数及其各种统计数据的估计

图20-模型的协整方程

图21:VECM的Akaike信息标准

根据在上述的数据，我们可以估计：

·?=

·?=,

·?=,and

·?=.

总的来说，结果表明该模型非常适合。协整方程中的ln(SF)系数和调整参数都具有统计显著性。调整参数表明，当协整方程的预测值为正数时，由于协整方程中的ln(value)系数为负，ln(value)低于其平衡值。系数L.ce1的估计值为-0.14。

因此，当比特币的价值过低时，它很快就会上升回到lnSF。系数L.ce1估计值为0.028，意味着当比特币价值过低时，它会向均衡方向调整。

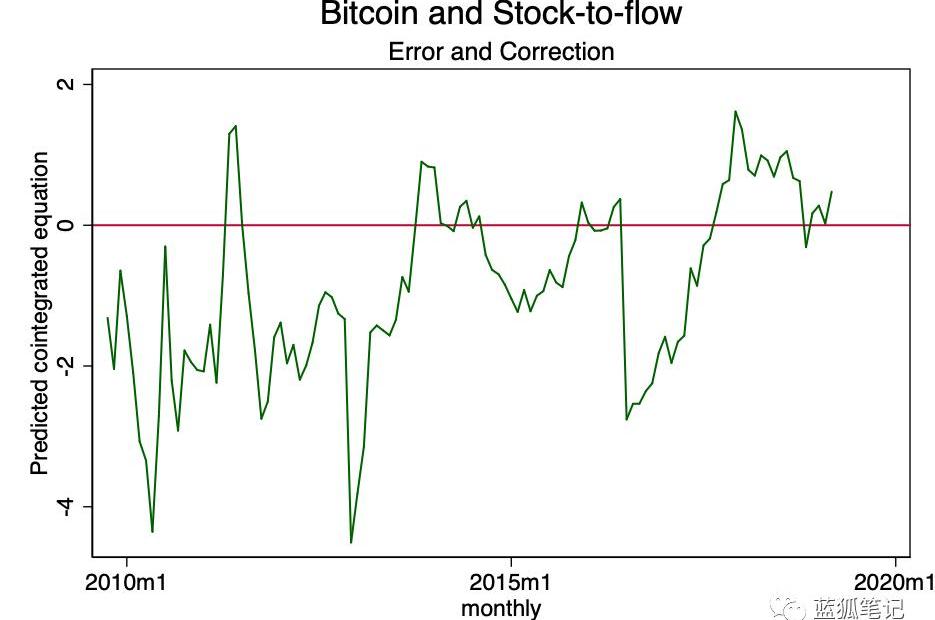
图22-协整方程随时间的估计

在上图中，我们可以看到协整方程是趋向于零的。虽然它在形式上可能不是静止的，但它确实在接近平稳状态。

来自STATA手册：

具有K个内生变量和r个协整方程的VECM伴随矩阵具有Kr单位特征值。如果过程是稳定的，则剩余r特征值的系数严格小于1。由于特征值的系数没有总分布，因此很难确定系数与另一个系数是否接近。

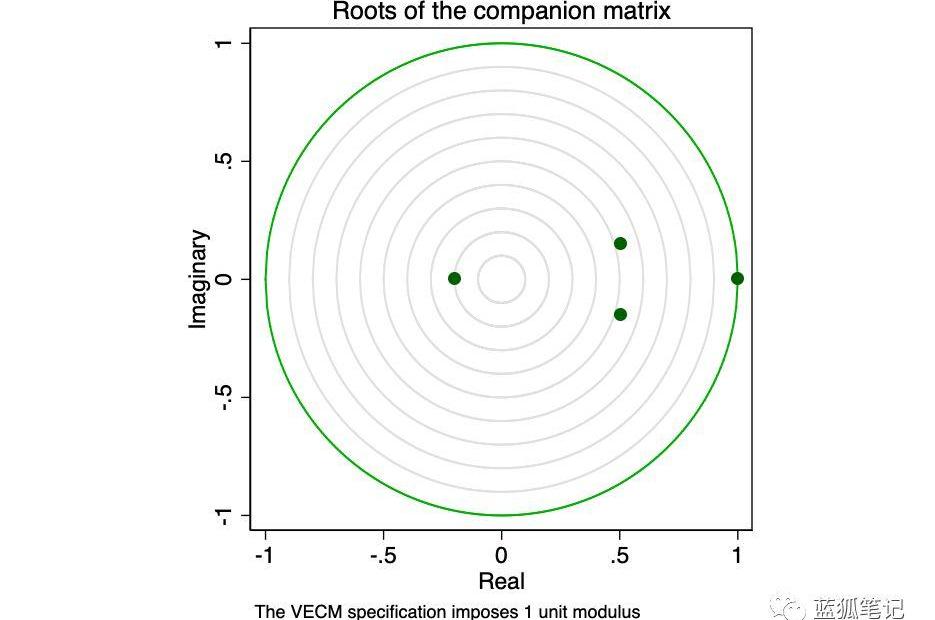
图23-伴随矩阵的根

特征值图显示，剩余特征值都不接近单位圆。稳定性检查并不能说明我们的模型是存在指定错误的。

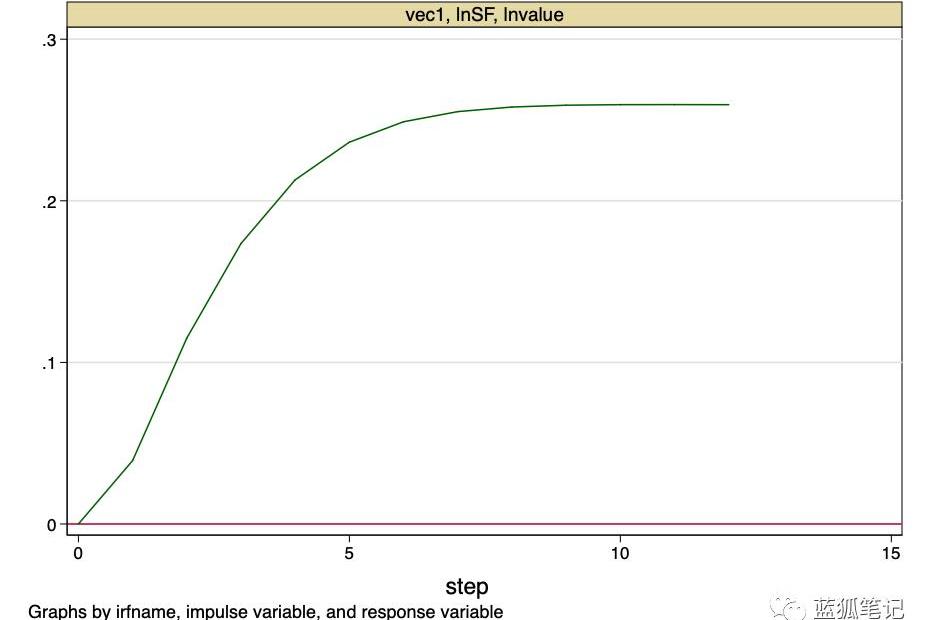
图24-脉冲响应函数

上图表明，stock-to-flow价值的正交冲击，对比特币的价值具有永久性影响。

这就是我们的底线。Stock-to-flow不是一个随机变量，它是一个随时间变化的已知值的函数。stock-to-flow不会受到冲击，即它的价值可以由提前计算得到精确值。然而，这个模型提供了非常有力的证据，证明了在stock-to-flow与比特币价值之间存在着一种基本的非虚假关系。

局限性

在这项研究中，我们没有考虑任何混淆变量。鉴于上述证据，任何混淆都不太可能对我们的结论产生重大影响——我们不能拒绝H0。我们不能说“stock-to-flow与比特币价值之间没有关系”。如果是这样的话，就不存在协整方程了。

结论

虽然本文提出的一些模型在Akaike信息准则方面超过了原始模型，但所有这些模型都未能否定“stock-to-flow是比特币价值的重要非虚假预测因素”的这个假设。

用一个比喻来说明这一点：如果我们把比特币的价值看作一个醉汉，那么stock-to-flow并不是他真正的跟班狗，而更像是他走的路。醉汉会在路上到处游荡，有时会停下来、滑倒、错过一个拐弯处、甚至在路上抄近路等；但总的来说，他会沿着这条路的方向回家。

简而言之，比特币就像是醉汉，而Stock-to-Flow就是回家的路。

------

风险警示：蓝狐笔记所有文章都不能作为投资建议或推荐，投资有风险，投资应该考虑个人风险承受能力，建议对项目进行深入考察，慎重做好自己的投资决策。

标签：比特币STOTOCFLO李晨比特币5个亿爆仓怎么翻身比特币MOONSTORMMoon Maker ProtocolFLAFLO

Gateio热门资讯